Математические модели в экономике Назад на образовательную программу
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ - МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ СТУДЕНТАМ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
Разделы
Список Литературы
- Гетманчук А. В.Экономико-математические методы и модели: учебное пособие для бакалавров / А. В. Гетманчук, М. М. Ермилов. - М. : Издательско-торговая корпорация «Дашков и К», 2013. - 188 с. - читать в библиотеке
- Хуснутдинов Р. Ш. Экономико-математические методы и модели : учебное пособие / Р.Ш. Хуснутдинов. - М.: НИЦ Инфра-М, 2013. - 224 с. - читать в библиотеке
- Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013. - 432 с. - ISBN 978-5-394-01943-2. - читать в библиотеке
- Балдин, К. В. Математическое программирование: Учебник / К. В. Балдин, Н. А. Брызгалов, А. В. Рукосуев; Под общ. ред. д.э.н., проф. К. В. Балдина. - 2-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 220 с. - ISBN 978-5-394-01457-4. - читать в библиотеке
Дополнительная литература
- Экономико-математические методы в примерах и задачах : учебное пособие / А.Н.Гармаш, И.В.Орлова, Н.В.Концевая и др. ; под ред. А.Н.Гармаша - М. : Вузовский учебник : НИЦ ИНФРА-М, 2014 – 416 с. - читать в библиотеке
- Экономико-математические методы и модели: компьютерное моделирование : учебное пособие / И.В. Орлова, В.А. Половников. - 3-e изд., перераб. и доп. - М. : Вузовский учебник : НИЦ ИНФРА-М, 2014. - 389 с. - читать в библиотеке

Ваш библиотекарь |
Внимание!Для входа в Электронную Библиотеку Вам нужно получить Логин и Пароль.
|
 |
Форма контроля
Форма отправки результатов (ТЕСТ, РЕФЕРАТ)
|
|

ВАШ Куратор(495) 632-00-78 |
Содержание разделов печать раздела -
Основы теории управления.
верх
Лекция 1: Понятие об управлении и сфера его применения.
В Элладе начала возникать наука (система правил), регламентирующих поведение гибернета ( лицо принимающее решения (ЛПР)) в тех или иных условиях. Эту науку собственно и стоило бы назвать кибернетикой. Для людей XIX века, получивших классическое образование, слово «кибернетика» было понятно и означало, систему взглядов которой должен был обладать управляющий, чтобы эффективно управлять своим гиберно (объект управления). Термин (по современным понятиям) означает теорию управления - причем не общую теорию, а управление объектами, основными элементами которых являются люди (технологическими системами) Гиберно - объект управления, содержащий людей. Воинская часть - это гиберно. Танк сам по себе как некоторая техническая система уже не гиберно, и механик-водитель - не гибернет. Но танк с экипажем - это гиберно, и его командир, который не только направляет танк, но и управляет экипажем, является гибернетом. В 1843 году в Познани выходит книга польского профессора философии Б. Трентовского «Отношение философии к кибернетике как искусству управления народом», содержащая изложение его университетского курса лекций по философии кибернетики.Общество и любая его часть (любой коллектив и любой индивид) - единство несопоставимого, а в снятии противоречий и заложено его развитие. Руководитель (по Б. Трентовскому – кибернет) должен примирять различные взгляды и стремления, использовать их на общее благо, создавать и направлять деятельность различных институтов так, чтобы из противоречивых стремлений рождалось бы согласованное поступательное движение. Для выработки сложного решения всегда нужен научный анализ. Б. Трентовский, рассуждая о науке управления, отдает должное роли таланта управляющего и термину «искусство управления», которым он широко пользуется. Это и есть основное отличие его кибернетики от древнегреческой. Управленческий процесс - не только совокупность административных акций. Чем дальше развивается общество, тем большую роль в управлении играет научный анализ, а ЛПР обретает черты ученого. Б. Трентовский понимал, что по мере продвижения человеческого общества по пути прогресса процесс управления все в большей степени приобретает черты научного исследования, а лицо получившее право управления постепенно становится все более похожим на ученого и, прежде чем принять то или иное решение, оно должно внимательно проанализировать обстановку и оценить возможные его последствия. При этом оно должно полагаться не только на свой опыт и свою интуицию, но и на научную теорию. Основной целью и объектом управления является, по мнению Б. Трентовского, человек. С одной стороны, кибернет должен уметь наблюдать, анализировать, выжидать, лавировать, избегать прямого вмешательства - он должен уметь извлекать пользу из естественного хода вещей; с другой - он должен быть активен: любое его решение должно носить «волевой характер», оно должно неукоснительно выполняться. Кибернет должен быть уверен, что подчиненные ему гиберно выполнят его распоряжение. Исполняющему всегда должен быть понятен смысл приказа, его цели, достигнутый результат и кара, которая может последовать за его невыполнением, - последнее обязательно. Кибернет при этом должен быть образцом для своих подчиненных - «следуй за мной и делай как я». Отданные приказы должны обязательно выполняться. Процесс управления не может существовать без известных заранее поощрений и наказаний. Законы развития общества объективны (на больших временных интервалах они не зависят от воли управляющих). Функция науки - помогать ему предвидеть возможные варианты развития событии. Задача кибернетики не просто формулировать общие соображения, а помогать исследователю (или управляющему) предвидеть будущее - следствия своих решений.
В 40-х годах XX века Н. Винер публикует ряд работ, посвященных кибернетике как науке об управлении и связи в животном мире и машинах. Его единомышленники стали расширять сферу приложения кибернетики при исследовании явлений общественного характера. Эта попытка встретила резкую критику со стороны ученых различных направлений, и, прежде всего, со стороны марксистов. Критика была отчасти мотивирована: расширение области применения идей Н. Винера не всегда учитывало объективных закономерностей общественного развития и носило механистический характер. Попытка идти от машины к обществу, представить происходящее в обществе в терминах технической дисциплины всегда неудачна. В трудах Б. Трентовского импонирует то, что он исходил от человека, от потребностей социума и от законов его эволюции. Практическое управление трактовало роль управляющего в раннем капиталистическом обществе примитивно: он должен был прежде всего уметь управлять - заставлять людей работать и обеспечивать эффективность предприятия. Становление капиталистического способа производства резко повысило интерес к тем вопросам управления, от которых зависела деятельность той или иной фирмы, предприятия, завода в условиях рынка. Управление сводилось прежде всего к созданию производственных структур обеспечивавших максимальную прибыль. Так философия и социальное управление, провозглашаемые Н. Макиавелли и идеальной системой Гегеля оказались невостребованными, ибо родилась научная организация труда. В 40-х годах XX века ситуация меняется. Быстрое развитие техники и технологии резко усложнило управленческие процессы. Рост концентрации производства, его специализация и необходимость учета огромных потоков информации обнаружили слабость прежних приемов управления, НОТ и других средств, традиционно применявшихся управляющими. Возникла необходимость научного подхода к делу управления. Поэтому второе рождение кибернетики и появление книги Н. Винера «Кибернетика и общество» было с энтузиазмом воспринято на Западе. Альтернативу кибернетике Н. Винера составляет синергетика Р.Б. Фулера, предложенная им в 40-х гг ХХ века, но оказавшаяся в полной мере востребованной только в 70-е гг, благодаря теоретическим изысканиям Л. фон Берталанфи, А.А. Богданова, Б. Мандельброта, Г. Хакена, И. Пригожина, В.И. Арнольда и появлению ЭВМ (для визуализации соответствующих нелинейным хаотическим системам фрактальных множеств).
Рекомендованная литература:
- Машунин Ю.К. Теория управления. Математический аппарат управления в экономике : учеб. посоюие / Ю.К. Машунин. – М.: Логос, 2013. – 448 с.
Лекция 2: Принцип обратной связи. Программный метод управления.
Принцип управления по отклонению (принцип обратной связи). Этот принцип является одним из наиболее ранних и широко распространенных принципов управления. В соответствии с этим принципом система управления наблюдает за объектом, на который воздействуют возмущающие факторы. В результате, в поведении объекта возникают отклонения. Система управления отслеживает наблюдаемые параметры (переменные) и на основе наблюдений создает алгоритм управления. Особенность этого принципа заключается в том, что система управления начинает действовать на объект только после того, как факт отклонения уже свершился. Это и есть "обратная связь". Схема управления изображена на рисунке. При такой схеме полная компенсация влияния возмущающих воздействий невозможна. Тем не менее, схема управления с обратной связью получила наибольшее распространение на практике. Это объясняется простотой ее реализации.Обратная связь — одно из основных понятий теории управления. Вообще обратной связью называется любая передача влияния из выхода той или другой системы на его вход. В системах управления обратная связь можно определить как информационную связь, с помощью которой в управляющую часть поступает информация о следствиях управления объектом, то есть информация о новом состоянии объекта, который возник под влиянием управляющих действий. Благодаря наличия обратной связи сложные системы в принципе могут выходить за пределы действий, которые предусмотренные и определенные их разработчиками. Ведь обратная связь создает в системе новое качество: способность накоплять опыт, определять свое будущее обращение в зависимости от обращения в минувшему, то есть самообучаться. Обратную связь можно обнаружить во многих процессах в природе. Примером могут служить вестибулярный аппарат, обнаруживающий отклонение тела от вертикали и обеспечивающий поддержание равновесия, системы регуляции температуры тела, ритма дыхания и т.д. В организациях обратная связь при управлении устанавливается посредством осуществления контроля исполнения. Принцип обратной связи является весьма универсальным фундаментальным принципом управления, действующим в технике, природе и обществе. Программно-целевое управление — управление, ориентирующееся на достижение конкретного конечного результата в решении определенной проблемы, развитии той или иной отрасли или региона и в заранее установленные сроки.
Основными принципами программно-целевого управления являются: ориентация на конечную цель, сквозное планирование объекта управления, принцип непрерывности. Программно-целевое управление предназначено для решения сложных проблем общественного производства, возникающих при реализации крупномасштабных народнохозяйственных, межотраслевых и межрегиональных целей с жесткими директивными сроками. Основными этапами программно-целевого управления являются: формулировка цели программы; декомпозиция (расчленение) цели на отдельные задачи и мероприятия — формирование дерева целей и задач и оценка его элементов; обоснование альтернативных направлений (средств) достижения целей программы; оптимизация распределения ресурсов между отдельными ветвями дерева целей и темпов финансирования; изменение приоритетности отдельных целей программы или средств их достижения; адаптация целевой части программы к изменяющимся внешним условиям. С усложнением задач развития и совершенствования производства роль программно-целевого управления возрастает. Принципы программно-целевого управления, разработка и осуществление комплексных целевых программ находят все большее распространение на всех уровнях управления — народном хозяйстве в целом, отраслях и регионах, объединениях и предприятиях. Систе́ма (от др.-греч. σύστημα — целое, составленное из частей; соединение) — множество элементов, находящихся в отношениях и связях друг с другом, которое образует определённую целостность, единство.
Модель — это материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале. Математические модели — некоторые целостные математические структуры в виде алгебраических, дифференциальных и других уравнений. Технологическая система – совокупность функционально-взаимосвязанных средств технологического оснащения, предметов производства и исполнителей для выполнения в регламентированных условиях производства заданных технологических процессов или операций. К предметам производства относят: материал, заготовку, полуфабрикат и изделие, находящееся в соответствии с выполняемым технологическим процессом в стадии хранения, транспортирования, формообразования, обработки, сборки, ремонта, контроля и испытаний. К регламентированным условиям производства относятся: регулярность поступления предметов производства, параметры энергоснабжения, окружающей среды и др.Рекомендованная литература:
- Машунин Ю.К. Теория управления. Математический аппарат управления в экономике : учеб. посоюие / Ю.К. Машунин. – М.: Логос, 2013. – 448 с.
Системный подход к моделированию объектов и систем управления
верх
Лекция 1: Риски и угрозы.
Модели для выявления и анализа возможностей, рисков и угроз. Управление рисками, риск-менеджмент (англ. risk management) — процесс принятия и выполнения управленческих решений, направленных на снижение вероятности возникновения неблагоприятного результата и минимизацию возможных потерь проекта, вызванных его реализацией. Современная экономическая наука представляет риск как вероятное событие, в результате наступления которого могут произойти только нейтральные или отрицательные последствия. (Если событие предполагает наличие как положительных, так и отрицательных результатов, и в отдельных изданиях именуется спекулятивным риском, то оно исследовано экспертами не добросовестно. Эти события (а не событие) имеют дуальную природу и всегда (!) могут быть разделены на «шанс» (предполагаемое событие, способное принести кому-либо полезность, выгоду, прибыль) и «риск» (предполагаемое событие, способное принести кому-либо ущерб, убыток). Дуальные события могут быть сопутствующими (реализация шанса может повлечь за собой риск или наоборот), взаимоисключающими (игра в орлянку) или независимыми (реализация шанса и риска не зависит друг от друга, а определяется обстоятельствами и неопределённостью). Именно поэтому, в целях создания стройной системы взглядов на риск-менеджмент, следует признать все риски чистыми, а дуальные события определённые как «спекулятивные» подвергать повторному анализу). Цель риск-менеджмента в сфере экономики — повышение конкурентоспособности хозяйствующих субъектов с помощью защиты от реализации чистых рисков. В риск-менеджменте принято выделять несколько ключевых этапов:- выявление риска и оценка вероятности его реализации и масштаба последствий, определение максимально-возможного убытка;
- выбор методов и инструментов управления выявленным риском;
- разработка риск-стратегии с целью снижения вероятности реализации риска и минимизации возможных негативных последствий;
- реализация риск-стратегии;
- оценка достигнутых результатов и корректировка риск-стратегии.
Ключевым этапом риск-менеджмента считается этап выбора методов и инструментов управления риском. Прогнозное планирование: определение рисков и поиск возможностей. Методы прогнозирования рисков. Теория риск-менеджмента основывается на трёх базовых понятиях: полезности, регрессии и диверсификации. Базовыми методами риск-менеджмента являются отказ от риска, снижение, передача и принятие.
Риск-инструментарий значительно шире. Он включает политические, организационные, правовые, экономические, социальные инструменты, причём риск-менеджмент как система допускает возможность одновременного применения нескольких методов и инструментов риск-управления. Наиболее часто применяемым инструментом риск-менеджмента является страхование. Страхование предполагает передачу ответственности за возмещение предполагаемого ущерба сторонней организации (страховой компании). Примерами других инструментов могут быть:- отказ от чрезмерно рисковой деятельности (метод отказа),
- профилактика или диверсификация (метод снижения),
- аутсорсинг затратных рисковых функций (метод передачи),
- формирование резервов или запасов (метод принятия).
Рекомендованная литература:
- Рыхтикова Н.А. Анализ и управление рисками организации : учеб. пособие / Н.А. Рыхтикова. – 2-е изд. – М.: Форум 2014. – 240 с.
Лекция 2: Экономико-математическое моделирование.
Применение аппарата дифференциальных уравнений в экономике.
Рассмотрим модель естественного роста выпуска. Предположим, что некоторая продукция продается по фиксированной цене Р. Обозначим через Q(t) количество продукции, реализованное на момент времени t. Получен доход PQ(t). Часть дохода расходуется на инвестиции в производство:
I(t)=mPQ(t),Преобразование Лапласа — интегральное преобразование, связывающее функцию F(s) комплексного переменного (изображение) с функцией f(x) вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Математические модели социоэкономических систем и вычислительных процессов. Классификация аппаратов математического моделирования и их взаимосвязь.
верх
Лекция 1:Понятие о математической модели экономических систем.
Экономические процессы в различных отраслях национального хозяйства представляют собой сложные явления, связанные с многочисленными факторами внутреннего и внешнего воздействия на производство, которые, как правило, изменяются с течением времени. Кроме того, эффективность процессов часто зависит от человеческого фактора, что значительно усложняет как разработку, так и интерпретацию полученных результатов моделирования. Так как реальный процесс или явление, как правило, сложная система взаимодействия внутренних и внешних частей и факторов, для их изучения абстрагируются от части взаимодействий и их природы, выделяя те из них, которые в настоящий момент интересуют исследователя. В этом случае принято говорить о модели явления или процесса. В дальнейшем будем называть модель процесса, явления или объекта кратко — модель объекта (МО). Термин «модель» широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений. Мы рассматриваем только те модели, которые строятся человеком и используются им в качестве инструмента получения знаний. Модель — это материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале. Процесс построения, изучения и применения моделей называется моделированием. Оно тесно связано с такими категориями, как абстракция, аналогия, гипотеза и др. Процесс моделирования обязательно включает и построение абстракций, и умозаключения по аналогии, и конструирование научных гипотез. Моделирование в экономике — это воспроизведение экономических объектов и процессов в ограниченных, малых, экспериментальных формах, в искусственно созданных условиях. В экономике чаще используется математическое моделирование посредством описания экономических процессов математическими зависимостями. Моделирование служит предпосылкой и средством анализа экономики и протекающих в ней явлений, а также методом обоснования принимаемых решений, прогнозирования, планирования, управления экономическими процессами и объектами. Модель экономического объекта обычно поддерживается реальными статистическими и эмпирическими данными, а результаты расчетов, выполненные в рамках построенной модели, позволяют строить прогнозы и давать объективные оценки исследуемых объектов. Объектом моделирования может быть либо реальная хозяйственная система, либо один или несколько процессов, протекающих в ней. Для построения модели необходимо не просто выбрать объект, но и дать его описание в виде системы, т.е. определить границы его взаимодействия с внешней средой, его структуру. Модели одного и того же объекта могут быть различными и отражать этот объект с разных сторон. Математические модели — некоторые целостные математические структуры в виде алгебраических, дифференциальных и других уравнений.
Чаще всего в экономических исследованиях применяются смешанные модели, например логико-математические, логико-иконографические и др. Математические модели в экономике имеют целевое назначение (например, для исследования структуры, функционирования, расхода).Модели структуры предназначены для изучения взаимоположения и связей элементов системы как внутри нее, так и с внешней средой. Такие модели могут быть представлены в виде сетевых моделей, графиков, матриц и др. Модели функционирования предназначены для изучения системы в динамике. Так, модели жизненного цикла изделий изучаются в маркетинге, модели операций применяются для решения конкретных экономических задач (модели анализа, прогнозирования, управления и др.). Модели расхода или прибыли используются при определении технико-экономических показателей систем, оптимизации по отдельным критериям и в других случаях.
При классификации моделей по исследуемым экономическим процессам и содержательной проблематике можно выделить модели макроэкономические и микроэкономические. Макроэкономические модели строятся на уровне национального хозяйства, а микроэкономические — на уровнях организаций, их объединений и отдельных регионов. Различают модели дескриптивные и нормативные.
Дескриптивные модели отвечают на вопросы: «Как это происходит?» или «Как это вероятнее всего может дальше развиваться?», т.е. они только объясняют наблюдаемые факты или дают вероятный прогноз. Применение дескриптивного подхода в моделировании экономики объясняется необходимостью эмпирического выявления отдельных факторов при изучении технологических процессов. Характерным признаком таких моделей в большинстве случаев является изменение параметров системы в функции от времени. Нормативные модели отвечают на вопрос: «Как это должно быть?», т.е. предполагают целенаправленную деятельность. Типичный пример нормативных моделей — модели оптимального планирования, формализирующие тем или иным способом цели экономического развития, возможности и средства их достижения. При изучении экономических процессов математические модели рассматриваются в тесной связи с целевыми системами и представляют собой некоторые целостные структуры (назовем их экономико-математическими моделями).
Экономико-математические модели (ЭММ) — смешанные модели (логико-математические, математико-иконографические и др.), включающие в себя совокупность математических зависимостей, логических построений, схем, графиков и т.д., связанных в некоторую единую систему, имеющую экономический смысл. По целевому назначению ЭММ делятся на теоретико-аналитические (используемые в исследованиях общих свойств и закономерностей экономических объектов) и прикладные (применяемые в решении различных зависимостей в экономике, в частности для установления статистических закономерностей экономического поведения социальных групп, вероятных путей развития каких-либо процессов при определенных условиях). Примерами дескриптивных моделей являются производственные функции и функции покупательского спроса, построенные на основе обработки статистических материалов. Является ли ЭММ дескриптивной или нормативной, зависит не только от ее математической структуры, но от характера использования данной модели. Например, модель межотраслевого баланса дескриптивна, если она используется для анализа пропорций прошлого периода. Но эта же математическая модель становится нормативной, когда она применяется для расчетов сбалансированных вариантов развития национального хозяйства, удовлетворяющих конечные потребности общества при плановых нормативных производственных затратах. По характеру отражения причинно-следственных связей выделяют модели жестко детерминистские и модели, учитывающие случайность и неопределенность. Различают неопределенности, описываемые вероятностными законами, и неопределенности, для описания которых вероятностные методы неприменимы. Второй тип неопределенности гораздо более" сложен для моделирования. По способам отражения фактора времени ЭММ делятся на статические и динамические. В статических моделях все зависимости относятся к одному моменту или периоду времени. Динамические модели характеризуют изменения экономических процессов во времени. Модели экономических процессов чрезвычайно разнообразны по форме математических зависимостей. Особенно следует выделить класс линейных моделей, наиболее удобных для анализа и вычислений, вследствие чего они получили наибольшее распространение. Различие между линейными и нелинейными моделями существенны не только с математической точки зрения, но и в теоретико-экономическом отношении, поскольку многие зависимости в экономике носят принципиально нелинейный характер: эффективность использования ресурсов при увеличении производства, изменение спроса и потребления населения при увеличении производства и т.д. Теория «линейной экономики» существенно отличается от теории «нелинейной экономики». По соотношению внешних и внутренних переменных, включаемых в модель, они могут разделяться на открытые и закрытые. Хотя полностью закрытых и открытых моделей почти не бывает. Большинство ЭММ занимают промежуточное положение и различаются по степени открытости или закрытости. При рассмотрении сложного объекта, как правило, прибегают к построению моделей его отдельных частей (так называемые детализированные модели). Из детализированных моделей, в свою очередь, составляется общая модель, называемая агрегированной.
ЭММ можно классифицировать и по другим признакам, например по отраслям, направлениям исследований, сложности, используемому математическому аппарату и т.д. Статистическое и эконометрическое модели́рование — исследование объектов познания на их статистических моделях; построение и изучение моделей реально существующих предметов, процессов или явлений (например: экономических процессов в эконометрике) с целью получения объяснений этих явлений, а также для предсказания явлений или показателей, интересующих исследователя. Оценка параметров таких моделей производится с помощью статистических методов. Например: метод максимального правдоподобия, метод наименьших квадратов, метод моментов. Пример статистической модели: линия регрессии (см. подробнее Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию [Электронный ресурс] : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013, стр. 346-350) Имитационная модель (ИМ) – это формальное (выполненное на формальном языке) описание логики функционирования исследуемой системы и взаимодействия, отдельных её элементов во времени, учитывающее наиболее существенные причинно – следственные связи, присущие данной системе, и обеспечивающие проведение статистических экспериментов.
При разработке ИМ остаются справедливыми основные принципы моделирования систем. Надо отметить два важных факта:- взаимосвязь между отдельными элементами системы, описанными в модели, а также между некоторыми величинами (параметрами) может быть представлена в виде аналитических зависимостей (например, при моделировании полета летательного аппарата обработка поступающих на борт команд может быть описана на уровне логики, а возникающие перегрузки рассчитываются аналитически);
- модель можно считать реализуемой и имеющей практическую только в том случае, если в ней отражены лишь те свойства реальной системы, которые влияют на значения выбранного показателя эффективности (ПЭ).
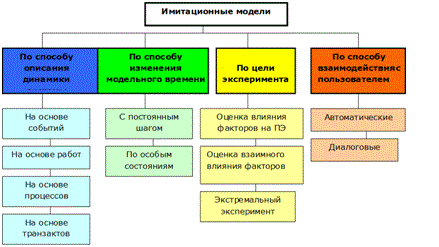
Для ИМ отсутствуют ограничения на область их применения (по типу моделируемой системы), и речь может идти только о целесообразности использования ИМ в данной предметной области и об объёме затрат на её разработку и реализацию. Основой имитационного моделирования является метод статистических испытаний и наибольший эффект от его применения достигается при исследовании сложных систем, на функционирование которых существенное влияние оказывают случайные факторы.
Применение ИМ целесообразно в следующих случаях:- нет законченной постановки задачи на исследование, и идет процесс познания объекта моделирования;
- характер протекающих в системе процессов не позволяет описать их в аналитической форме;
- необходимо наблюдать за поведением системы (или отдельных ее компонент) за определённый период, в т.ч. с изменением скорости протекания процессов;
- при изучении новых ситуаций в системе либо при оценке функционирования ее в новых условиях;
- исследуемая система является элементом более сложной системы, другие элементы которой уже реализованы;
- исследуется относительное влияние различных факторов на значения выходных характеристик системы;
- определяется аналитическая зависимость между интересующими исследователя выходными характеристиками и факторами;
- определяются оптимальные значения параметров системы («экстремальный эксперимент»).
Рекомендуемая литература:
- Гетманчук А. В.Экономико-математические методы и модели: учебное пособие для бакалавров / А. В. Гетманчук, М. М. Ермилов. - М. : Издательско-торговая корпорация «Дашков и К», 2013. - 188 с.
- Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013. - 432 с. - ISBN 978-5-394-01943-2.
Лекция 2: Математические модели оптимальных управляемых процессов.
Оптимальное управление — это задача проектирования системы, обеспечивающей для заданного объекта управления или процесса закон управления или управляющую последовательность воздействий, обеспечивающих максимум или минимум заданной совокупности критериев качества системы. Для решения задачи оптимального управления строится математическая модель управляемого объекта или процесса, описывающая его поведение с течением времени под влиянием управляющих воздействий и собственного текущего состояния. Математическая модель для задачи оптимального управления включает в себя: формулировку цели управления, выраженную через критерий качества управления; определение дифференциальных или разностных уравнений, описывающих возможные способы движения объекта управления; определение ограничений на используемые ресурсы в виде уравнений или неравенств. Все задачи оптимального управления можно рассматривать как задачи математического программирования и в таком виде решать их численными методами.
При оптимальном управлении иерархическими многоуровневыми системами, например, крупными химическими производствами, металлургическими и энергетическими комплексами, применяются многоцелевые и многоуровневые иерархические системы оптимального управления. В математическую модель вводятся критерии качества управления для каждого уровня управления и для всей системы в целом, а также координация действий между уровнями управления. Если управляемый объект или процесс является детерминированным, то для его описания используются дифференциальные уравнения. Наиболее часто используются обыкновенные дифференциальные уравнения вида x'(t) = a(x(t),u(t),t). В более сложных математических моделях (для систем с распределёнными параметрами) для описания объекта используются дифференциальные уравнения в частных производных. Если решение поставленной задачи оптимального управления не является непрерывно зависящим от исходных данных (некорректная задача), то такая задача решается специальными численными методами.
Система оптимального управления, способная накапливать опыт и улучшать на этой основе свою работу, называется обучающейся системой оптимального управления. Реальное поведение объекта или системы всегда отличается от программного вследствие неточности в начальных условиях, неполной информации о внешних возмущениях, действующих на объект, неточности реализации программного управления и т.д. Поэтому для минимизации отклонения поведения объекта от оптимального обычно используется система автоматического регулирования Иногда (например, при управлении сложными объектами, такими как доменная печь в металлургии или при анализе экономической информации) в исходных данных и знаниях об управляемом объекте при постановке задачи оптимального управления содержится неопределённая или нечёткая информация, которая не может быть обработана традиционными количественными методами. В таких случаях можно использовать алгоритмы оптимального управления на основе математической теории нечётких множеств (Нечёткое управление). Используемые понятия и знания преобразуются в нечёткую форму, определяются нечёткие правила вывода принимаемых решений, затем производится обратное преобразование нечётких принятых решений в физические управляющие переменные.
Лекция 3 «Транспортная модель»
Транспортная задача. Пусть в пунктах отправления A1,…,Am содержится груз в количествах a1,…,am > 0 единиц соответственно. Этот груз перевозится в пункты назначения B1,…,Bn, где он полностью потребляется в количествах b1,…,bn > 0 единиц соответственно. Для каждой пары индексов i,j задана стоимость cij 0 перевозок единицы груза из пункта отправления Ai в пункт назначения Bj. Требуется найти такой план перевозок X, чтобы его стоимость была бы минимальной, причем весь груз из пунктов A1,…,Am необходимо перевезти в пункты назначения B1,…,Bn таким образом, чтобы потребности каждого из пунктов B1,…,Bn были полностью удовлетворены.
Назовем планом перевозок неотрицательную матрицу X = (xij) размера m*n, в которой число xij ≥ 0 указывает количество груза, перевозимого из пункта Ai в пункт Bj, 1 ≤ i ≤ m, 1 ≤ j ≤ n.
Стоимость z(X) перевозок является линейной функцией от X, именно, z(X) = ∑i,j cijxij, xij ≥ 0.
В задаче требуется найти такой план перевозок X, чтобы его стоимость была бы минимальной, причем весь груз был бы вывезен из пунктов отправления, доставлен в пункты назначения, и все потребности были бы полностью удовлетворены. То, что весь груз, содержащейся в Ai вывозится записывается в виде уравнения.
∑jxij = ai , ( i = 1, …, m )
Аналогично, условие того, что потребности пункта Bj полностью удовлетворены, записывается в виде уравнения
∑i xij = bj, ( j = 1, …, n ).
Таким образом, транспортная задача записывается следующим образом
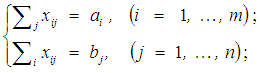
xij ≥ 0;
z(X) = ∑i,j cijxij → min.

План перевозок X называется допустимым, если он удовлетворяет системе ограничений (1). Допустимый план Х,* при котором целевая функция принимает минимальное значение, называется оптимальным.
Теорема 1. Транспортная задача (1) имеет решение тогда и только тогда, когда
т.е. общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления.
Если ∑i ai = ∑j bj, то модель транспортной задачи называется закрытой. Если указанное условие не выполнено, то модель транспортной задачи называется открытой.
Чтобы решить открытую модель транспортной задачи ее необходимо свести к закрытой модели.
В случае превышения запаса над потребностью, т.е. ∑i ai > ∑j bj вводится фиктивный (n+1) – й пункт назначения с потребностью bn+1= ∑i ai - ∑j bj и все тарифы считаются равными нулю, т.е. ci n+1=0 (i=1,..,m).
Аналогично, если ∑i ai ˂ ∑j bj, то вводится фиктивный (m+1) – пункт отправления с запасом груза am+1= ∑j bj - ∑i ai и тарифы полагаются равными нулю, т.е. cm+1 j=0 (j=1,…,n).
Таким образом, открытая модель транспортной задачи превращается в закрытую модель транспортной задачи.
Укажем способ построения допустимого решения методом минимального элемента.
Этот способ возможен, если ∑i ai = ∑j bj. Для этого выберем клетку с индексами (i,j), в которой стоит минимальное из чисел cij. В эту клетку помещаем число xij = min(ai ,bj ). Если ai bj, то все остальные элементы i-ой строки полагаем равными нулю, число bj заменяем на bj – ai, а ai на 0. Если же ai ≥ bj, то все остальные элементы j-ого столбца полагаем равными нулю, число ai заменяем на ai – bj, а bj на 0. В результате число пустых строк или столбцов уменьшается на единицу. Продолжая этот процесс, получаем первоначальный план.
Метод северо-западного угла (см. Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013. - 432 с. - ISBN 978-5-394-01943-2, стр. 378)
Метод потенциалов (см. Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013. - 432 с. - ISBN 978-5-394-01943-2, стр. 380-386)
Рекомендованная литература
- Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013. - 432 с. - ISBN 978-5-394-01943-2.
- Балдин, К. В. Математическое программирование: Учебник / К. В. Балдин, Н. А. Брызгалов, А. В. Рукосуев; Под общ. ред. д.э.н., проф. К. В. Балдина. - 2-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 220 с. - ISBN 978-5-394-01457-4.
Математическое программирование.
верх
Лекция 1 «Линейное и целочисленное программирование»
Линейное программирование - область математики, разрабатывающая теорию и численные методы решения задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных, если функция и ограничения линейны относительно входящих в задачу неизвестных . Функцию, экстремальное значение которой нужно найти в условиях экономических возможностей, называют целевой функцией (функцией цели). Математическая модель задачи линейного программирования включает в себя следующие пункты:
- Совокупность неизвестных величин X=(x1,x2,…,xn), действуя на которые, систему можно совершенствовать. Их называют планом задач (вектором управления, решением, стратегией, поведением и т.д.);
- Целевую функцию Z(X) (функция цели, показатель эффективности, критерий оптимальности). Она позволяет выбрать наилучший вариант из множества возможных вариантов. Наилучший вариант дает целевой функции экстремальное значение (max или min). С экономической точки зрения целевая функция может отображать объем выпуска или реализации продукции, затраты и прибыль, издержки обращения, уровень обслуживания или уровень дефицитности, отходы и т.д.
- Условия (или система ограничений) налагаемые на неизвестные величины. Они вытекают из ограниченности ресурсов, необходимости удовлетворения потребностей, из условий производства. Ограничениями также являются возможности технического, технологического и научного потенциала, а не только материальные, финансовые и трудовые ресурсы. Нередко потребности превышают возможности. В этом случае математические ограничения выражаются в виде неравенств. Совокупность условий образует область допустимых решений (область экономических возможностей) G: x
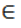 G
G
На план задачи, исходя из экономических или физических условий, могут быть наложены условия неотрицательности (xi ≥0) или условия целочисленности (xi КАРТИНКА Z). Ограничения вида: или - называются тривиальными. Эти ограничения записывают обычно в конце системы ограничений задачи линейного программирования (ЛП). Все остальные ограничения называются нетривиальными. План X, удовлетворяющий системе ограничений задачи, называется допустимым планом. Допустимый план, в котором целевая функция принимает экстремальное значение, называется оптимальным и обозначается X*.
Необходимо найти план, при котором целевая функция достигает экстремального значения max (min) z=Z(x), x ![]() G
при ограничениях φi(x1,x2,…,xn)≥{≤,=}b.
G
при ограничениях φi(x1,x2,…,xn)≥{≤,=}b.
Пример задачи линейного программирования.
Пусть предприятие выпускает к-типов продукции, используя т-видов ресурсов. При этом расход i-го вида ресурса на единицу j-го вида продукции составляют aij ; всего имеется объем bi запаса i-го вида ресурса; реализация единицы продукции j-го вида дает cj условных денежных единиц прибыли. Требуется составить оптимальный план выпуска продукции. Модель задачи имеет в этом случае вид:
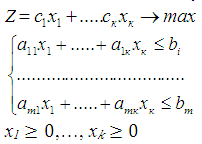
где x1,.......,xk - объемы планируемого выпуска продукции.
Формы записи задач линейного программирования
- Общая задача ЛП может быть представлена в виде:
- Задача ЛП называется однородной (симметричной), если все ограничения имеют вид неравенства.
- Задача ЛП называется канонической, если все нетривиальные ограничения имеют вид равенства и на все переменные наложены тривиальные ограничения.
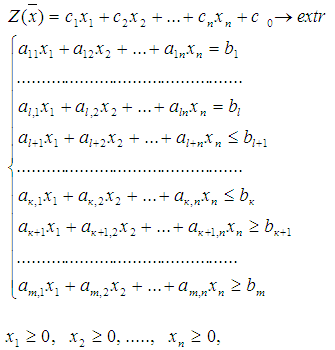
Частными случаями однородной задачи являются задача о ресурсах (или производственная) и задача об издержках: В первом случае требуется найти максимум функции Z («прибыли») при ограниченных «ресурсах» bi, во втором – минимум издержек Z при заданных «нормах потребления» bi
Любую задачу ЛП можно привести к канонической форме и обратно. Геометрическая интерпретация и графическое решение ЗЛП Если однородная ЗЛП содержит две переменные, то она может быть решена графически. Постановка ЗЛП в этом случае имеет вид
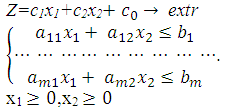
Непустое множество допустимых планов называется многогранником решений, а всякая угловая точка многогранника решений называется вершиной.
Вектор ![]() координатами из коэффициентов cj при переменных xj целевой функции Z называется вектором роста целевой функции:
координатами из коэффициентов cj при переменных xj целевой функции Z называется вектором роста целевой функции: ![]() Он показывает направление наибольшего возрастания целевой функции, а вектор( -
Он показывает направление наибольшего возрастания целевой функции, а вектор( - ![]() ) – направление наибольшего убывания целевой функции.
Уравнение h = c1x1 + c2x2 при фиксированном h=h0 определяет на плоскости прямую h0 = c1x1 + c2x2, называемую линей уровня. При изменении h получаем семейство линий уровня, т.е. семейство параллельных прямых.
Вектор роста
) – направление наибольшего убывания целевой функции.
Уравнение h = c1x1 + c2x2 при фиксированном h=h0 определяет на плоскости прямую h0 = c1x1 + c2x2, называемую линей уровня. При изменении h получаем семейство линий уровня, т.е. семейство параллельных прямых.
Вектор роста![]() перпендикулярен к каждой из линий уровня.
перпендикулярен к каждой из линий уровня.
Теорема: Если ЗЛП имеет решение, то целевая функция достигает экстремального значения в одной из вершин многогранника решений.
Так как система ограничений есть система линейных неравенств, то областью допустимых значений неизвестных является выпуклая многоугольная область, лежащая в первой четверти. Оптимальное значение целевая функция принимает в вершинах области решений, поэтому можно предложить следующий план графического решения задачи (см. подробнее Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013. - 432 с. - ISBN 978-5-394-01943-2. стр. 371-372):
- построить область решений системы ограничений,
- построить вектор роста,
- построить линию уровня,
- параллельным переносом этой прямой в направлении вектора роста, определить наибольшее (наименьшее) значение целевой функции в одной из вершин многоугольника решений.
Симплекс - метод решения ЗЛП
Область допустимых решений задачи линейного программирования образует выпуклый многогранник в n-мерном пространстве, если условия задачи линейного программирования не противоречивы. При этом оптимальное решение, если оно существует, обязательно достигается в некоторой вершине многогранника (возможно, и более чем в одной). Но в этом случае, чтобы найти решение задачи линейного программирования необходимо перебрать все планы, соответствующие вершинам многогранника допустимых решений. Такие планы называются опорными. Однако в сложных задачах число вершин может оказаться чрезмерно большим, вследствие чего, нахождение всех опорных планов потребует огромного объема вычислений. Метод, который позволяет осуществить упорядоченный перебор вершин многогранника аналитически, выполняя элементарные алгебраические преобразования, является симплексный метод. После определения одной из вершин многогранника, этот метод позволяет установить, является ли найденный план оптимальным, т.е. достигнут ли в этой вершине максимум (минимум) целевой функции. В основе симплексного метода лежит алгоритм симплексных преобразований системы уравнений, приведенной к единичному базису, дополненный правилом, обеспечивающим переход не к любому , а к «лучшему» опорному решению.
Найти максимальное значение целевой функции
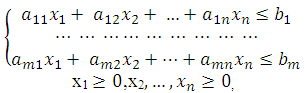
Алгоритм симплекс-метода (см. подробнее Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013. - 432 с. - ISBN 978-5-394-01943-2. стр. 372-375).
- Составить первый опорный план.
- Проверить оптимальность опорного плана.
- Определить разрешающий элемент.
- Определить новый опорный план и проверить его на оптимальность.
Если критерий оптимальности не выполнен, то ищем следующий опорный план и так до тех пор, пока не будет найдено оптимальное решение.
Теорема 1. Если в индексной строке оптимального плана имеется хотя бы одно нулевое значение, соответствующее свободной переменной, то задача линейного программирования имеет бесчисленное множество оптимальных планов. Если ЗЛП имеет бесконечное множество оптимальных планов, можно сказать, что с экономической точки зрения решение задачи возможно, но оно не единственное.
Теорема 2. Если в индексной строке содержится отрицательный элемент (при исследовании задачи на максимум), а в соответствующем разрешающем столбце нет ни одного положительного элемента, то целевая функция на множестве допустимых решений неограниченна сверху, т.е. Z(X)→∞. Задача не имеет решения. С экономической точки зрения неограниченность целевой функции говорит о том, что разработанная модель недостаточно точна, т.е. нет полного учета ограничений, которые являются существенными в данной задаче. Если в оптимальном плане возникла дополнительная переменная, это говорит о том, что при реализации данного плана останутся неиспользованные ресурсы.
Целочисленное программирование (см. подробнее Балдин, К. В. Математическое программирование: Учебник / К. В. Балдин, Н. А. Брызгалов, А. В. Рукосуев; Под общ. ред. д.э.н., проф. К. В. Балдина. - 2-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 220 с. - ISBN 978-5-394-01457-4. стр. 86-96).
В ряде экономических задач, относящихся к задачам линейного программирования, элементы решения должны выражаться в целых числах. В этих задачах переменные означают количество единиц неделимой продукции.
Найти такое решение план Х=(х1, х2,…, хn), при котором линейная функция Z=c1x1+c2x2…+cn xn+ c0 принимает максимальное или минимальное значение при ограничениях
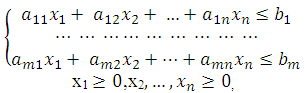
х1,х2,…, хn целые числа
Задача решается методами линейного программирования. В случае если переменные оптимального решения оказываются нецелочисленными, то, применяют метод отсечения или метод перебора целочисленных решений.
Рекомендованная литература:
- Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013. - 432 с. - ISBN 978-5-394-01943-2.
- Балдин, К. В. Математическое программирование: Учебник / К. В. Балдин, Н. А. Брызгалов, А. В. Рукосуев; Под общ. ред. д.э.н., проф. К. В. Балдина. - 2-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 220 с. - ISBN 978-5-394-01457-4.
Лекция 2 «Нелинейное и динамическое программирование»
Во многих оптимизационных задачах целевая функция, или функции, задающие ограничения, не являются линейными. Такие задачи называются задачами нелинейного программирования. (см подробнее Балдин, К. В. Математическое программирование: Учебник / К. В. Балдин, Н. А. Брызгалов, А. В. Рукосуев; Под общ. ред. д.э.н., проф. К. В. Балдина. - 2-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 220 с. - ISBN 978-5-394-01457-4.стр. 130-142)
Пример простой нелинейной задачи: Предприятие для производства какого-то продукта расходует два средства в количестве х и y соответственно. Это факторы производства, например, машины и труд, два различных вида сырья и т.п., а х и y – затраты факторов производства. Факторы производства считаются взаимозаменяемыми. Если это «труд» и «машины», то можно применять такие методы производства, при которых величина затрат в сопоставлении с величиной затрат труда оказывается больше или меньше (производство более или менее трудоемкое). Объем производства, выраженный в натуральных или стоимостных единицах, является функцией затрат производства Z = f (х, y). Эта зависимость называется производственной функцией. Совокупные издержки выражаются формулой с1х1 + с2y2 = в. Требуется при данных совокупных издержках определить количество факторов производства, которое максимизирует объем продукции Z.
Математическая модель задачи:
Определить такие переменные х и у, удовлетворяющие условиям с1х1 + с2у=в, х≥0, у≥0, при которых функция z=f(х, у) достигнет максимума.
Ограничения могут отсутствовать. В этом случае производится безусловная оптимизация задачи. Как правило, функция z может иметь произвольный нелинейный вид. В теории нелинейной оптимизации выделяют понятие локального экстремума (локального минимума, локального максимума), глобального экстремума, условного экстремума. Понятие условного экстремума вводится для случая, когда число переменных n не меньше 2 (n≥2).
Динамическое программирование – раздел оптимального программирования (оптимального управления), в котором процесс принятия решения и управления, может быть разбит на отдельные этапы (шаги). (См. подробнее Балдин, К. В. Математическое программирование: Учебник / К. В. Балдин, Н. А. Брызгалов, А. В. Рукосуев; Под общ. ред. д.э.н., проф. К. В. Балдина. - 2-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 220 с. - ISBN 978-5-394-01457-4. стр. 142-161) Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческого решения.
Принцип оптимальности Беллмана.
Основным методом динамического программирования является метод рекуррентных соотношений; который основывается на использовании принципа оптимальности, разработанного американским математиком Р.Беллманом.
Суть принципа: Каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце каждого шага. Использование данного принципа гарантирует, что управление, выбранное на любом шаге, не локально лучше, а лучше с точки зрения процесса в целом.
Рекомендованная литература:
- Гетманчук А. В.Экономико-математические методы и модели: учебное пособие для бакалавров / А. В. Гетманчук, М. М. Ермилов. - М. : Издательско-торговая корпорация «Дашков и К», 2013. - 188 с.
- Балдин, К. В. Математическое программирование: Учебник / К. В. Балдин, Н. А. Брызгалов, А. В. Рукосуев; Под общ. ред. д.э.н., проф. К. В. Балдина. - 2-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 220 с. - ISBN 978-5-394-01457-4.
Лекция 3 « Сетевые методы анализа и управления»
Основные понятия метода сетевого планирования (См. подробнее Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013. - 432 с. - ISBN 978-5-394-01943-2.стр. 389-398)
При сетевом планировании определяются оценки продолжительности операций, и строится сетевая модель – сетевой график. Построение сетевого графика позволяет проанализировать все операции и внести улучшения в структуру модели до начала ее реализации. Календарный сетевой график определяет начало и окончание каждой операции, а также взаимосвязи с другими операциями графика. Он выявляет критические операции, которым надо уделять особое внимание, чтобы закончить все работы в директивный срок. По выявленным некритическим операциям календарный сетевой график позволяет определить резервы времени, которые можно выгодно использовать при задержке выполнения работ или эффективном использовании трудовых и финансовых ресурсов.Сетевой график (сетевая модель) – графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого планирования лежит изображение планируемого комплекса работ в виде графа.
Граф – схема состоящая из заданных точек (вершин), соединенных системой линий. Ориентированным называется такой граф, на котором стрелкой указаны направления всех его ребер (дуг), что позволяет определить какая из двух его граничных вершин является начальной, а какая конечной.
Сетевой график – это ориентированный граф без контуров (в контуре начальная вершина совпадает с конечной). Основными элементами сетевых графиков являются: работа, события, путь.
Работа – это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.
Фиктивная работа – это связь между результатами работ (событиями), не требующая затрат времени и ресурсов, т.е. имеющая нулевую продолжительность.
Событие – это результат выполнения одной или нескольких предшествующих работ.
Путь – любая непрерывная последовательность (цепь) работ и событий.
Критический путь – это путь не имеющий резервов работы комплекса. Работы расположенные на критическом пути, называют критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.
Ожидание – процесс, требующий затрат времени, но не требующий затрат ресурсов (отдых персонала, ожидание благоприятных условий и т.п.).
Все работы изображаются на сетевом графике стрелками, величина которых не зависит от продолжительности работы и расхода ресурсов. Стрелки указывают факт и направление движения процесса. Фиктивная работа изображается пунктирной стрелкой. У всех стрелок проставляются индексы, соответствующие наименованию работы, а под ними - время, затрачиваемое на данную работу. Понятие событие отличается от понятия работы тем, что не является процессом и не связано с затратами времени и ресурсов (разработка сметы закончена, ресурс принят, сборка узла машины завершена). Оно может иметь следующие значения:
- Исходное событие, с которого начинаются все работы. В исходное событие не входит ни одна работа (например, получено распоряжение о начале производства продукта).
- Завершающее событие – событие, которым заканчивается весь комплекс работ и из него не выходит ни одной работы.
- Промежуточные события, или просто события – все события, находящиеся между исходным и завершающим событием.
Любая работа соединяет только 2 события. Событие, из которого выходит работа, является для него начальным или последующим, а куда входит – конечным или последующим. Работы сетевого графика обозначаются большими буквами и кодируются начальными i и конечными j событиями (А04; А01; А23;…). События сетевого графика обозначаются малыми буквами и нумеруются в порядке последовательности развития операции.
Путь в сетевом графике – любая последовательность работ, в которой конечное событие каждой работы является началом следующей за ней работы. Наибольший по продолжительности путь называется критическим и обозначается L кр, а его продолжительность Т кр. Выделение критического пути является важнейшим элементом в сетевом планировании.
Критический путь позволяет:
- Определить какие работы и события лимитируют выполнение всего комплекса работ;
- Позволяет сосредоточить внимание руководителя не на всех работах, а прежде всего на лежащих на критическом пути;
- Помогает ускорить выполнение работ за счет привлечения резервов, скрытых в некритических работах.
Рекомендованная литература
- Гетманчук А. В.Экономико-математические методы и модели: учебное пособие для бакалавров / А. В. Гетманчук, М. М. Ермилов. - М. : Издательско-торговая корпорация «Дашков и К», 2013. - 188 с.
- Шапкин, А. С. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию : Учебное пособие для бакалавров / А. С. Шапкин, В. А. Шапкин. - 8-е изд. - М. : Издательско-торговая корпорация «Дашков и К°», 2013. - 432 с. - ISBN 978-5-394-01943-2.
- Балдин, К. В. Математическое программирование: Учебник / К. В. Балдин, Н. А. Брызгалов, А. В. Рукосуев; Под общ. ред. д.э.н., проф. К. В. Балдина. - 2-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 220 с. - ISBN 978-5-394-01457-4.