Основные понятия теории вероятностей.
верх

Сферы применения вероятностно-статистических методов. Дискретное вероятностное пространство. Случайные события и операции над ними. Вероятностное пространство. Вероятности и правила действий с ними. Независимость событий. Условная вероятность. Формула полной вероятности. Формула Байеса. Схема испытаний Бернулли. Непрерывное вероятностное пространство. Аксиоматика Колмогорова.

 

Лекция 1: «Основные понятия теории вероятностей»

 

Теория вероятностей – раздел математики, изучающий закономерности случайных явлений.

Под опытом, экспериментом, испытанием будем понимать осуществление конкретного комплекса условий.

Событием называется всякий исход испытания.

Событие называется случайным, если в результате опыта оно может произойти, а может и не произойти.

Событие называется достоверным, если оно происходит всегда при выполнении комплекса условий.

Невозможное событие – такое событие, которое никогда не происходит при выполнении комплекса условий.

Событие, которое невозможно разложить на более простые, называется элементарным. Все остальные события называются составными.

Множество всех элементарных событий в условиях данного эксперимента называется пространством элементарных событий.

Элементарные события называются в некотором опыте равновозможными, если в силу условий проведения опыта можно считать, что ни одно из них не является объективно более возможным, чем другие.

Пусть N − общее число равновозможных элементарных исходов в пространстве элементарных исходов Ω, а N_A − число элементарных исходов, образующих событие A или, как говорят, благоприятствующих событию A.

Вероятностью P (A) события A называют отношение числа N_A благоприятствующих событию A элементарных исходов к общему числу N равновозможных элементарных исходов:

P (A) = N/N_A .

Сформулированное определение вероятности принято называть классическим определением вероятности.

События обозначают латинскими буквами А, В, С, . . ., а вероятность буквой Р.

Два события называются совместными в данном опыте, если появление одного из них не исключает появления другого.

Два события называются несовместными в данном опыте, если они не могут произойти вместе при одном и том же испытании. 

П р о т и в о п о л о ж н ы м (или дополнительным) к событию A называется событие Ā состоящее в том, что событие A в результате эксперимента не произошло.

Несколько событий в условиях данного опыта образуют полную группу событий, если в результате опыта обязательно произойдет хотя бы одно из них.

События называются независимыми, если появление события В не оказывает влияния на вероятность события А.

События А₁, А₂, …, А_n называются попарно независимыми, если любая пара их независима.

События Н₁, Н₂, …, Н_n называются гипотезами, если они попарно независимы и образуют полную группу событий.

События называются зависимыми, если появление события В оказывает влияние на вероятность события А.

Суммой (объединением) двух событий А и B (обозначается А + В) называется событие, состоящее из всех элементарных исходов, принадлежащих по крайней мере одному из событий А или B. 

Произведением (пересечением) (обозначается А · В) событий А и B называется событие, состоящее из всех тех элементарных исходов, которые принадлежат и А и B. 

Свойства вероятности события.

1. Вероятность любого события есть неотрицательное число.

2. Вероятность достоверного события равна единице.

3. Вероятность невозможного события равна нулю.

4. Вероятность случайного события A есть число, заключенное между нулем и единицей.

5. Вероятность суммы двух несовместных событий равна сумме их вероятностей.

P(A + B) = P(A) + P(B).

6. Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности совмещения.

Р( А + В ) = Р( А ) + Р( В ) – Р( А∙В )

7. Если события А₁, А₂, …, А_n образуют полную группу, то

Р(А₁+ А₂+ …+ А_n) = 1

8. P(Ā) = 1 − P(A).

9. Если события А и В независимы, то вероятность их произведения равна произведению вероятностей

Р( А∙В ) = Р( А ) ∙ Р( В ).

Формула полной вероятности.

Вероятность события А при условии, что событие В произошло, называется условной вероятностью.

Обозначение: Р(А/В)

Если события А и В зависимы, то Р( А∙В ) = Р( А ) ∙ Р( В/А ).= Р(В) ∙ Р(А/В)

Формула полной вероятности события А запишется в виде

Р( А ) = 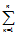Р( Н_к ) ∙ Р( А/Н_к ),

где Р( Н_к ) – вероятность гипотезы Н_к, а Р( А/Н_к ), – условная вероятность события А.

Формула Байеса.

Р(Н_к/А) =

Формула Байеса дает возможность переоценить условные вероятности гипотез Н_к.

Формулы Бернулли и Пуассона.

Если проводятся n (n<10) независимых испытаний, в результате в каждом из которых может появиться событие А с вероятностью p и не появиться с вероятностью q = 1 – p, то вероятность появления события А ровно m раз в n испытаниях вычисляют по формуле Бернулли

P_n( m ) = C_n^m ∙p^m ∙ q^n–m.

Если при этом число испытаний велико, вероятность р события в одном испытании мала, а произведение np не превосходит 20, то вероятность P_n( m ) находится по приближенной формуле Пуассона

P_n( m ) = 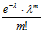, m = 0, 1, . . . n., где λ = np

    

Рекомендованная литература:

1. Балдин, К. В. Теория вероятностей и математическая статистика: Учебник / К. В. Балдин, В. Н. Башлыков, А. В. Рукосуев. - 2-е изд. - М.: Дашков и К, 2010. - 473 с. - ISBN 978-5-394-00617-3.

Случайные величины.
верх

Случайные величины. Функция распределения случайной величины. Функция плотности. Понятие о случайном векторе. Совместное распределение нескольких случайных величин. Независимость случайных величин. Маргинальные распределения. Условное распределение.

Лекция 1: «Случайные величины. Основные понятия.»

Случайной величиной называют величину, которая в результате испытания принимает то или иное возможное значение, причем заранее, до опыта, неизвестно какое именно. Обычно рассматривают два типа случайных величин: дискретные и непрерывные.

Случайная величина называется дискретной, если множество ее значений является конечным или счетным.

Законом распределения дискретной случайной величины Х называется всякое соотношение между всеми возможными ее значениями х₁, х₂, . . . , х_n и соответствующими им вероятностями.

Закон распределения дискретной случайной величины Х чаще всего записывается в виде таблицы:

В этой таблице x_i - значения, которые может принимать случайная величина, p_i - соответствующая им вероятность.

Функцией распределения F(х) случайной величины Х, называется вероятность того, что Х примет значение меньшее чем произвольное действительное число х.

Непрерывной называется случайная величина Х, если ее функция распределения непрерывна. Распределение непрерывной случайной величины однозначно определяется ее функцией распределения.

Свойства функции распределения (см. подробнее Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика, стр. 55- 60)

Р( a ≤ X ≤ b ) = F( b ) – F( a ).

Плотностью распределения f( х ) ( плотностью вероятности) непрерывной случайной величины Х называется производная ее функции распределения.

f( х ) = F'(х)

Свойства плотности вероятностей (см. подробнее Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика, стр. 60-62)

Рекомендованная литература:

1. Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика [Электронный ресурс] : учебник / К. В. Балдин, В. Н. Башлыков, А. В. Рукосуев. - 2-е изд. - М. : Дашков и К, 2010. - 473 с. 

Лекция 2: «Характеристики распределений случайных величин»

Математическое ожидание дискретной случайной величины Х определяется формулой М(Х) = 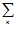x_кр_к. и имеет смысл среднего значения случайной величины.

Для оценки степени рассеивания значений случайной величины вокруг ее среднего значения вводится понятие дисперсии.

Дисперсия есть математическое ожидание квадрата разности случайной величины и ее математического ожидания.

D(X) = M(Х – M(Х))² = 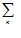(x_к – М(Х))²∙р_к.

Для вычисления дисперсии используют более удобную формулу

D(X) = M(Х²⁾ – (М(Х))².

Средним квадратическим отклонением называется величина σ = 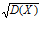, которая также является мерой рассеивания случайной величины Х.

Модой дискретной случайной величины называется значение, вероятность которого наибольшая.

Математическое ожидание непрерывной случайной величины, имеющей плотность f( х ) , определяется формулой М(Х) = 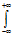хf( х )dx ,

Дисперсия непрерывной случайной величины, имеющей плотность f( х ) , определяется формулой

D(X) = M( Х – M(Х))² = 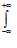x² f( x )dx – (М(Х))².

Средним квадратическим отклонением называется величина σ = .

Медианой M_l случайной величины называется такое ее значение для которого Р(х ≤ M_l) ≥ 0,5; Р(х ≥ M_l) ≥ 0,5

Свойства математического ожидания и дисперсии (см. Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика, стр. 114-117)

Рекомендованная литература:

1. Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика [Электронный ресурс] : учебник / К. В. Балдин, В. Н. Башлыков, А. В. Рукосуев. - 2-е изд. - М. : Дашков и К, 2010. - 473 с. 

Лекция 3: «Основные законы распределений случайных величин» (см. подробнее Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика, стр. 74-88)

Биноминальное распределение.

Случайная величина имеет биноминальное распределение тогда, когда вероятность находится по формуле Бернулли

P_n( m ) = C_n^m ∙p^m ∙ q^n–m.

М(Х) = nр, D(Х) = npq.

Распределение Пуассона.

Случайная величина имеет распределение Пуассона тогда, когда вероятность находится по формуле Пуассона

P_n( m ) = 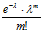, m = 0, 1, . . . n., где λ = np

М(Х) = D(Х) = λ.

Равномерное распределение.

Распределение случайной величины называется равномерным на [a,b], если ее плотность вероятности имеет вид:

f(x) =

M(X) = , D(X) =

Экспоненциальное (показательное) распределение.

Распределение случайной величины называется экспоненциальным, если ее плотность вероятности имеет вид:

f(t) = le^-lt , t ≥ 0, где λ – параметр распределения, λ > 0.

Математическое ожидание и дисперсию случайной величины находят по формулам:

M(t) = 1/λ, D(t) = 1/ λ².

Нормальное распределение.

Распределение случайной величины называется нормальным если ее плотность распределения имеет вид:

f(t)= , где а и σ – параметры распределения (математическое ожидание и среднее квадратическое отклонение) , a > 0, σ > 0,

Рекомендованная литература:

1. Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика [Электронный ресурс] : учебник / К. В. Балдин, В. Н. Башлыков, А. В. Рукосуев. - 2-е изд. - М. : Дашков и К, 2010. - 473 с. 

Предельные теоремы.
верх

Виды сходимости последовательности случайных величин. Неравенство Чебышева. Закон больших чисел и его следствия. Особая роль нормального распределения: центральная предельная теорема. Теоремы Муавра-Лапласа (локальная и интегральная).

Лекция 1: «Предельные теоремы». (см. подробнее Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика, стр. 217-222)

Неравенство Чебышева. Теорема Чебышева.

Для дискретных и непрерывных случайных величин справедливо неравенство Чебышева.

Пусть дискретная случайная величина X задана следующей таблицей распределения:

Требуется оценить вероятность того, что отклонение случайной величины от ее математического ожидания не превосходит по абсолютной величине положительного числа ε. Если ε довольно мало, то мы оценим вероятность того, что X примет значения, довольно близкие к своему математическому ожиданию. П. Л. Чебышев доказал неравенство, благодаря которому можно дать интересующую нас оценку.

Неравенство Чебышева. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше, чем (1—D(X))/ε²:

P(| X −M(X )| <ε)≥(1−D(X) )/ε²

Теорема Чебышева. если рассматривается достаточно большое число независимых случайных величин, которые имеют ограниченные дисперсии, то почти достоверным можно считать событие, заключающееся в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Локальная теорема Лапласа.

Использование формулы Бернулли при больших значениях n довольно проблематично, поскольку формула требует выполнения действий над гигантскими числами. При подсчете такого рода величин накапливаются погрешности, и окончательный результат может значительно отличаться от действительного. Чтобы найти интересующую вероятность, не обязательно пользоваться формулой Бернулли. Это можно сделать в соответствии с локальной теоремой Лапласа, которая дает асимптотическую формулу. Данная формула позволяет приблизительно найти вероятность появления события ровно k раз в n испытаниях при условии, что число испытаний довольно велико. Эту теорему также называют теоремой Муавра — Лапласа.

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании неизменна и не равна нулю и единице, то в таком случае вероятность Р_n(k) того, что событие А появится в n испытаниях ровно k раз, приблизительно равна:

Р_n(k) ≈ ,

где

Интегральная теорема Лапласа.

Пусть производится n испытаний, причем в каждом из них вероятность появления события А неизменна и равна р (0 < р < 1).

Для того чтобы найти вероятность Р_n(k_l, k₂) того, что событие А появится в n испытаниях не менее k₁ и не более k₂ раз, воспользуемся интегральной теоремой Лапласа.

Теорема. Если вероятность р наступления события А в каждом испытании неизменна и не равна нулю и единице, то вероятность Р_n(k_l, k₂) того, что событие А появится в n испытаниях от k₁ до k₂ раз, приблизительно равна:

Р_n(k_l, k₂) ≈ φ( x^'') – φ( x′), где x′=(k₁−np)/ npq и x^{'' = (}k₂−np)/ npq.

Рекомендованная литература:

1. Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика [Электронный ресурс] : учебник / К. В. Балдин, В. Н. Башлыков, А. В. Рукосуев. - 2-е изд. - М. : Дашков и К, 2010. - 473 с. 

Математическая статистика
верх

Генеральная совокупность, выборка. Гистограмма и полигон частот. Выборочная (эмпирическая) функция распределения. Вариационный ряд. Выборочные характеристики (выборочное среднее и выборочная дисперсия) и их распределения для нормальной генеральной совокупности. Асимптотические свойства выборочных моментов.

Лекция 1: «Математическая статистика»

Статистической совокупностью называется совокупность предметов или явлений, объединенных каким-либо общим признаком. Обработка статистических данных приводит к установлению определенных закономерностей, присущих массовым явлениям.

Генеральная совокупность – совокупность объектов или наблюдений, все элементы которой подлежат изучению при статистическом анализе.

Выборка (х₁^', х₂^', …, х_n ^') объема n - результат n наблюдений (измерений), проведенных над исследуемой случайной величиной (генеральной совокупностью) Х.

Выборки в МС должны быть репрезентативны (представительны). Это означает, что:

• должен быть обеспечен полностью случайный выбор n значений;
• выборка должна иметь достаточно большой объем (обычно n > 40–50).

  Вариационным рядом называется последовательность элементов выборки, расположенных в неубывающем порядке. Одинаковые элементы повторяются.

  Операция расположения случайной величины по неубыванию называется ранжированием статистических данных.

  Следующий этап обработки ряда х₁^', х₂^', …, х_n ^'— составление статистического ряда распределения. Форма его записи зависит от характера изучаемой случайной величины Х.

  Пусть х — дискретная случайная величина и среди вариационного ряда встречаются одинаковые значения случайной величины. Тогда составляют дискретный статистический ряд который показывает, с какой частотой наблюдалось то или иное значение.

  

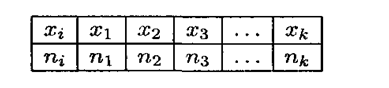
  х₁, х₂, ..., х_k – значения, которые принимает случайная величина, называются вариантами.

  n₁, n₂, ..., n_k – числа, показывающие сколько раз встречался соответствующий вариант, называются частотами.

  n₁ + n₂ + … + n_k = n - объем выборки.

  p_i^* = n_i/n –называется относительной частотой.

  Когда величина Х является непрерывной случайной величиной, тогда составляют интервальный статистический ряд. (см. подробнее Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика, стр. 232-235)

  Для графического изображения вариационных рядов используют гистограммы, полигон частот и кумуляту.

  Числовые характеристики вариационных рядов.

  Основной характеристикой вариационного ряда является его средняя арифметическая, называемая также выборочным средним.

  Для дискретного ряда она равна

  ,

  а для интервального ряда

  ,

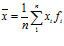  где x_i – середина i-го интервала, f_i – высота интервала, к – номер интервала.

  Выборочной дисперсией служит величина

  D = .

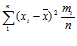  В статистическом анализе рассматривается также коэффициент вариации, равный отношению выборочного среднего квадратического отклонения к выборочной средней ν = 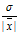(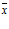¹ 0).

  Оценка параметров генеральной совокупности.(см. подробнее Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика, стр. 236-263)

  Пусть распределение случайной величины в генеральной совокупности зависит от какого-либо параметра θ. Оценкой 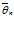параметра θ называется функция от значений выборки 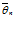( x₁, x₂, . . . , x_n ). Оценка 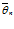называется несмещенной, если М 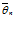= θ. Здесь устраняется возможность появления систематической ошибки при оценке параметра θ. Оценка 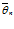называется состоятельной, если при больших n отклонение от θ становится сколь угодно малым.

  Оценкой качества несмещенной оценки является ее дисперсия. Она называется эффективной, если ее дисперсия D 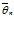= M(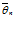 – θ )² является наименьшей среди дисперсий всех возможных оценок параметра θ.

  Основными статистическими распределениями являются

  а) распределение χ_n²;

  б) распределение Стьюдента t_n;

  в) распределение Фишера.

  Интервальные оценки параметров.

  Интервальной оценкой параметра θ называется интервал ( a,β ), который с заданной вероятностью γ покрывает неизвестное значение параметра θ.

  Такой интервал называется доверительным интервалом, а вероятность γ – доверительной вероятностью или уровнем надежности.

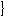
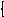  P| 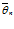– θ | < ∆ = γ тогда интервал имеет вид ( 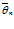– ∆ , 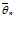+ ∆ ), то есть неравенства 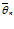– ∆ < θ < 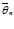+ ∆ выполняются с вероятностью γ.

  Проверка статистических гипотез.(см. подробнее Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика, стр. 268-306)

  Статистической гипотезой называется любое предположение о свойствах распределения вероятностей, лежащего в основе наблюдаемых явлений. Гипотезы обозначают латинскими буквами H₀, H₁, H₂, . . ., H_к. Гипотеза H₀ называется основной. Ей противопоставляются гипотезы, которые называются альтернативными.

  Вероятность отвергнуть гипотезу H₀, если она верна ( то есть принять гипотезу H₁ ), называется ошибкой первого рода или уровнем значимости и обозначается a

  P( H₁ / H₀ ) = a

  Величина 1 – a равна вероятности принять верную гипотезу и называется уровнем доверия

  P( H₀ / H₀ ) = 1 – a = γ

  Вероятность принять основную гипотезу, если она неверна, называется ошибкой второго рода и обозначается β P( H₀ / H₁ ) = β.

  Вероятность принять гипотезу H₁, если она верна, называется мощностью критерия P( H₁ / H₁ ) = 1 – β.

   

  Рекомендованная литература:

1. Рукосуев А. В., Балдин, К. В. Теория вероятностей и математическая статистика [Электронный ресурс] : учебник / К. В. Балдин, В. Н. Башлыков, А. В. Рукосуев. - 2-е изд. - М. : Дашков и К, 2010. - 473 с.