Логика как наука.
верх

Лекция 1: Логика как наука.

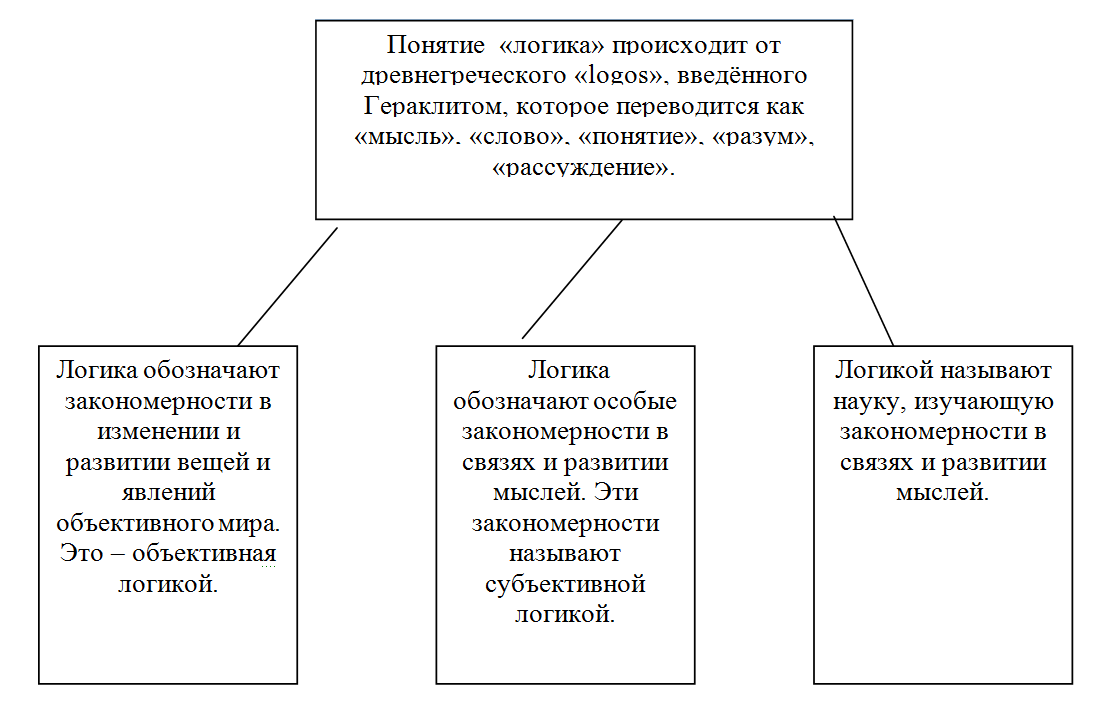
Слово «логика»происходит от древнегреческого слова «logos», введённого в оборот древнегреческим философов Гераклитом. Понятие «логика» в настоящее время употребляется в следующих смыслах:

• объективная логика – рассматривает закономерности в изменении и развитии вещей и явлений объективного мира;
• субъективная логика – рассматривает особые закономерности в связях и развитии мыслей.

Основоположником логики как самостоятельной науки является древнегреческий философ Аристотель (IV в. до н.э.). Логику Аристотеля принято называть традиционной формальной логикой. Традиционная формальная логика включала и включает такие разделы, как понятие, суждение, умозаключение, законы логики, доказательство и опровержение, гипотеза. Формальная логика – это наука о правильных формах мышления. Из самого названия следует, что данный вид логики преимущественное внимание уделяет формам мышления. Правильное мышление – это мышление, удовлетворяющее трём главным требованиям: определённости, последовательности и доказательности. Определённое мышление – это мышление точное, свободное от всякой сбивчивости. Последовательное мышление – это мышление, свободное от внутренних противоречий, разрушающих связь между мыслями там, где эта связь необходима. Доказательное мышление – это мышление, не просто формулирующее истину, но также указывающее основания, по которым она необходимо должна быть признана истиной. Непосредственной задачей логики является изучение форм мышления, отражающего и познающего действительность. Основными формами мышления являются понятия, суждения, умозаключения. Соблюдение законов логики – необходимое условие достижения истины в процессе мышления.

Схема № 1. Значение термина «Логика».

Парадоксы. Апории. Софизмы.
верх

Лекция 1: Парадоксы. Апории. Софизмы.

Парадокс – (от греческого слова «противоречия») это утверждение, которое расходится с общепринятым, устоявшимся мнением; суждения, которые являются противоположными, но для каждого из них есть убедительные аргументы. Апории – это неразрешимые противоречия. Апории были сформулированы древнегреческим философом Зеноном Элейским. Зенон сформулировал более 40 апорий, из них наиболее известны – «Дихотомия», «Стадий», «Стрела». В античной Греции высоко ценились учителя, их называли софистами (от греческого «софия» – мудрость), что означало первоначально «мудрец» или «учитель мудрости». Софисты учили детей грамоте, основам наук, воспитывали умение ясно и убедительно говорить, отстаивать в спорах своё мнение. Со временем, однако, софисты стали изобретать приёмы, направленные на то, чтобы одурачить собеседника, представить противника в смешном или глупом виде. Такие недобросовестные приёмы и уловки получили наименование «софизмы», а слово «софист» приобрело тот негативный оттенок, который сохранился у него до сих пор. Вот примеры некоторых софизмов, сохранившихся в трудах древних авторов: «То, чего ты не терял, у тебя есть. Ты не терял рогов. Следовательно, ты рогат». «Сидящий встал. Кто встал, тот стоит. Следовательно, сидящий стоит». Отношения между софизмами и парадоксами – ещё одна тема, не получающая своего развития в рамках традиционного истолкования софизмов. От софизма парадокс отличается формой. Софизм рассматривает противоречие, но выглядит, как рассуждение, в котором скрыто противоречие. Парадоксы же строятся на логической ошибке, которая не видна. Многие парадоксы казались неразрешимыми, и лишь с развитием логики и математики их удавалось решить. Парадокс лжеца «Я лгу. Но, если я лгу и сообщаю, что я лгу, то я говорю правду. А если я говорю правду, то какой же я лжец?» Данный парадокс решается переходом из одного семантического поля в другое. Следует ограничить значение высказывания «я лгу», например, «я сейчас лгу», т.е. введением нового слова уточнить значение предыдущего.

Серьёзным исследованием парадоксов занялись лишь в XIX веке, когда математика обратилась к логике, а логика – к математике. Английский философ, логик и математик Бертран Рассел обнаружил возможность решать парадоксы путём перехода из одного семантического поля в другое. Также Рассел является автором серии парадоксов, которые так и называются «Парадоксы Рассела». Парадокс «Брадобрей». Брадобрей бреет тех, кто не бреется сам. Бреет ли он себя? Парадокс «мэр города». Каждый мэр города живёт или в своём городе или вне его. Был издан приказ о выделении одного специального города, где бы жили только мэры, не живущие в своём городе. Где должен жить мэр этого специального города?

Понятие как форма мышления.
верх

Лекция 1: Понятие как форма мышления.

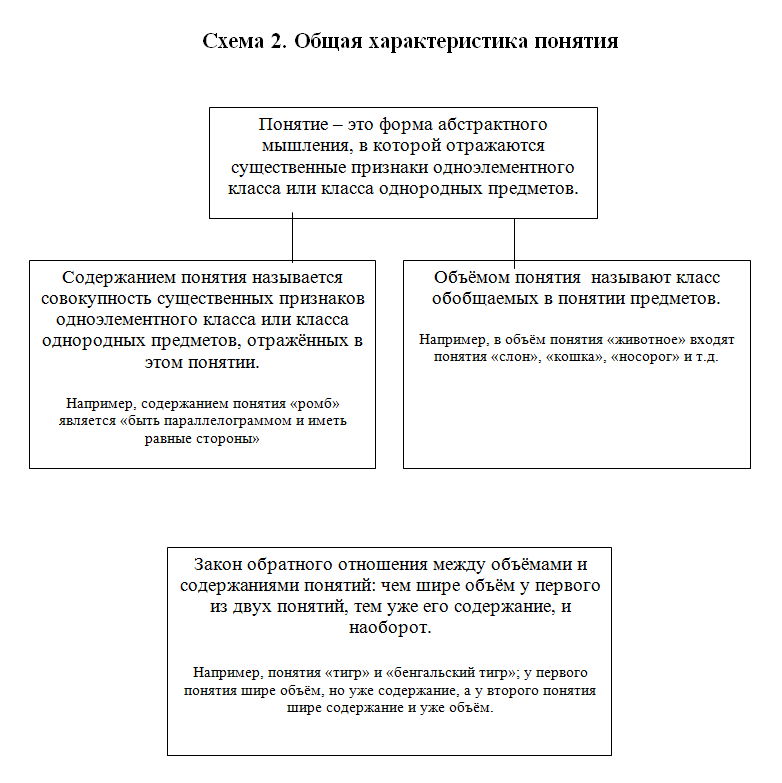
Понятие – это форма абстрактного мышления, в которой отражаются существенные признаки одноэлементного класса или класса однородных предметов. Существенные признаки – это такие признаки, каждый из которых, взятый отдельно, необходим, а взятые все вместе достаточны, чтобы с их помощью можно было отличить (выделить) данный предмет от всех остальных и обобщить однородные элементы в класс. Языковыми формами выражения понятий являются слова или словосочетания.

Основными логическими приёмами формирования понятий являются анализ, синтез, сравнение, абстрагирование, обобщение. Анализ – мысленное расчленение предметов на их составные части, мысленное выделение в них признаков. Синтез – мысленное соединение в единое целое частей предмета или его признаков, полученных в процессе анализа. Сравнение – мысленное установление сходства или различия предметов по существенным или несущественным признакам. Абстрагирование – мысленное выделение одних признаков предмета и отвлечение от других. Часто задача состоит в выделении существенных признаков предметов и в отвлечении от признаков несущественных, второстепенных. Обобщение – мысленное объединение отдельных предметов в некотором понятии.

Всякое понятие имеет содержание и объём. Содержанием понятия называется совокупность существенных признаков одноэлементного класса или класса однородных предметов, отражённых в этом понятии. Например, содержанием понятия «слон» будет совокупность следующих признаков: «крупное животное, серого цвета, имеющее хобот и большие уши».

Объёмом понятия называют класс обобщаемых в нём предметов. Например, в объём понятия «рыба» войдут объёмы таких понятий, как «карась», «щука», «окунь» и т.д. Объём понятия и его содержание взаимосвязаны между собой. Эта взаимосвязь именуется законом обратного отношения между объёмом и содержанием понятия: чем шире объём у первого из двух понятий, тем уже его содержание, и наоборот, чем шире содержание у первого из двух понятий, тем уже его объём. В этом законе речь идёт о понятиях, находящихся в родо-видовых отношениях. Например, понятия «часы» и «электронные часы»: у первого понятия, «часы», объём будет шире, чем у второго понятия, «электронные часы», а у понятия «электронные часы» шире будет содержание. Понятия можно классифицировать по объёму и по содержанию.

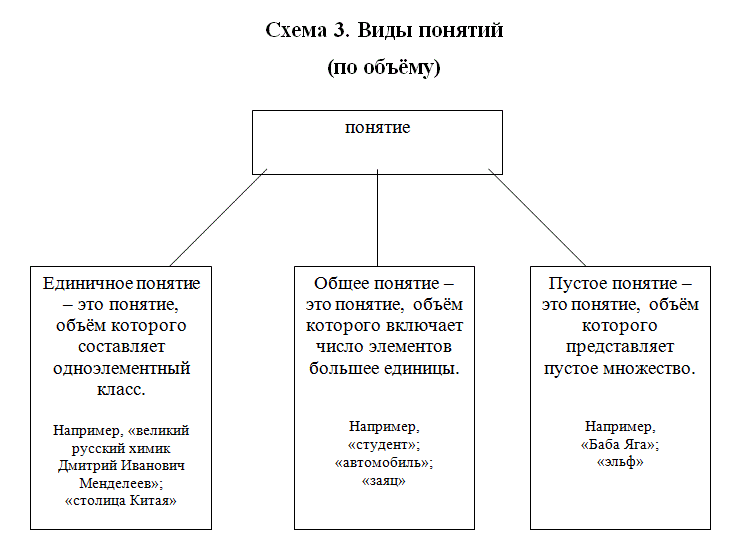
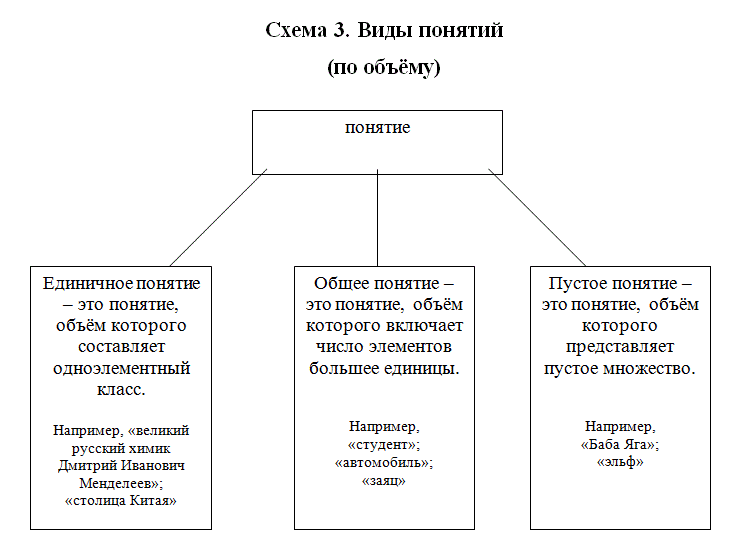
По объёму понятия делятся на единичные, общие и пустые. Объём единичного понятия составляет одноэлементный класс, то есть объем данного понятия равен единице (например, «великий русский химик Дмитрий Иванович Менделеев»). Объём общего понятия включает число элементов, большее единицы (например, «автомобиль»). Пустое понятие (понятие с нулевым объёмом) – это понятие, объём которого представляет пустое множество (например, «Баба Яга», «эльф», «вечный двигатель»).

По содержанию можно выделить следующие четыре пары понятий:

• конкретные – абстрактные понятия
• относительные – безотносительные понятия
• положительные – отрицательные понятия
• собирательные – несобирательные понятия

Конкретными называют понятия, в которых отражены одноэлементные или многоэлементные классы предметов, как материальные, так и идеальные (например, «дом», «наука»). Абстрактными называются те понятия, в которых мыслится не целый предмет, а какой-либо из признаков предмета, взятый отдельно от самого предмета (например, «несправедливость»). Относительные – это такие понятия, в которых мыслятся предметы, существование одного из которых предполагает существование другого (например, «дети» – «родители»). Безотносительные – такие понятия, в которых мыслятся предметы, существующие самостоятельно, вне зависимости от другого предмета (например, «человек»). Положительные понятия характеризуют в предмете наличие того или иного качества или отношения (например, грамотный человек; скупость).

Отрицательными называются те понятия, которые означают, что указанное качество отсутствует в предметах (например, «неграмотный человек»).

Собирательными называются понятия, в которых группа однородных предметов мыслится как единое целое (например, «дубовая роща»). Несобирательное понятие – это понятие, содержание которого можно отнести к каждому предмету данного класса, мыслимого в понятии (например, «ручка»).

Отношения между понятиями.
верх

Лекция 1: Отношения между понятиями.

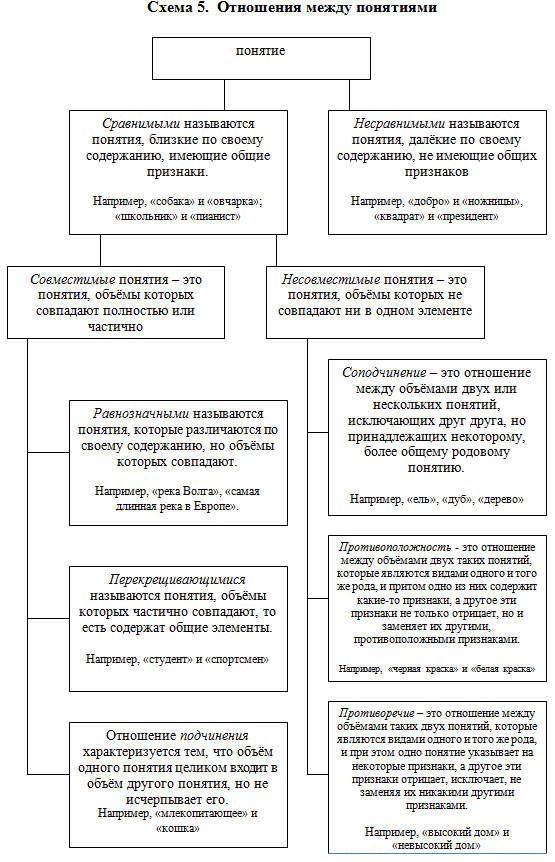
По содержанию понятия могут быть либо сравнимыми между собой, либо несравнимыми.

Несравнимыми называются понятия, далёкие по своему содержанию, то есть не имеющие общих признаков (например, «добро» и «ножницы»). Сравнимыми называются понятия, близкие по своему содержанию, то есть имеющие общие признаки (например, «птица» и «ворона»). Сравнимые понятия делятся по объёму на совместимые понятия и понятия несовместимые.

Совместимые понятия – это понятия, объёмы которых совпадают полностью или частично (например, «мебель» и «стол»). Несовместимые понятия – это понятия, объёмы которых не совпадают ни в одном элементе (например, «умный человек» и «глупый человек»). Отношения между объемами понятий изображаются с помощью круговых схем, кругов Эйлера, где каждый круг обозначает объём понятия. Само название «круги Эйлера» происходит от имени великого математика XVIII в. Леонарда Эйлера, который впервые предложил изображать объём понятия круговыми схемами.

Совместимые понятия бывают:

• равнозначные (тождественные)
• подчинённые
• перекрещивающиеся

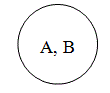
Равнозначными (тождественными) называются понятия, которые различаются по своему содержанию, но объёмы которых совпадают, то есть в них мыслится или одноэлементный класс, или один и тот же класс предметов, состоящий более, чем из одного элемента (например, А – «река Волга», В – «самая длинная река в Европе»).

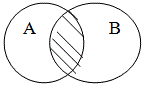
Понятия, объёмы которых частично совпадают, то есть содержат общие элементы, находятся в отношении перекрещивания, пересечения (например, А – «студент» и В – «спортсмен»).

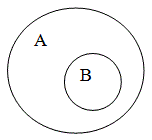
Отношение подчинения (субординации) характеризуется тем, что объём одного понятия целиком включается (входит) в объём другого понятия, но не исчерпывает его; это отношение вида и рода (например, В – «кошка» и А – «млекопитающее».)

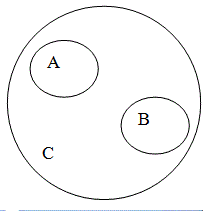
Несовместимые понятия бывают либо соподчинённые, либо противоположные, либо противоречащие. Соподчинение – это отношение между объёмами двух или нескольких понятий, исключающих друг друга, но принадлежащих некоторому, более общему родовому понятию (например, А – «ель», В – «берёза» принадлежат объёму понятия С – «дерево»).

В отношении противоположности (контрарности) находятся объёмы двух таких понятий, которые являются видами одного и того же рода, и притом одно из них содержит какие-то признаки, а другое эти признаки не только отрицает, но и заменяет их другими, исключающими, то есть противоположными признаками (например, А – «большой дом» и В – «маленький дом»).

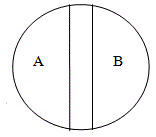
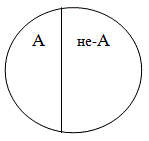
В отношении противоречия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками (например, А – «высокий дом» и не-А – «невысокий дом»).

Суждение как форма мышления. Простое суждение.
верх

Лекция 5: Суждение как форма мышления. Простое суждение.

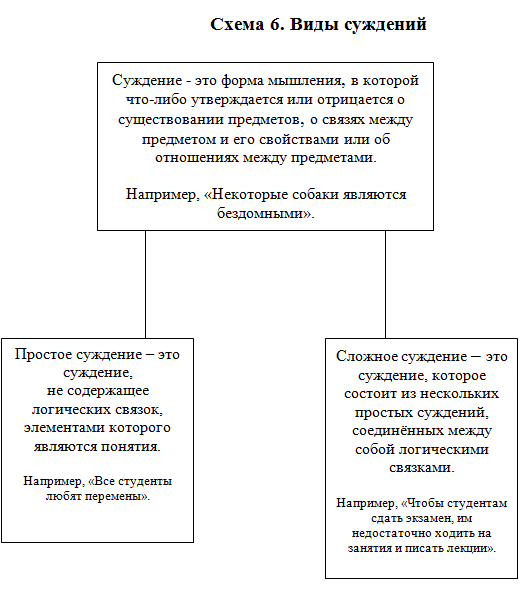
Суждение – это форма мышления, в которой что-либо утверждается или отрицается о существовании предметов, связях между предметом и его свойствами или об отношениях между предметами (например, «Некоторые деревья не являются лиственными»). В естественном языке суждение выражается посредством повествовательного предложения.

Традиционная логика является двузначной, так как в этой логике суждение имеет одно из двух значений истинности: оно либо истинно, либо ложно. Если в суждении утверждается или отрицается наличие у предмета какого-то признака, или констатируется существование какого-то предмета, или устанавливается отношение между предметами и это соответствует действительности, то суждение истинно (например, «Все ужи пресмыкающиеся»).

Суждения бывают простыми и сложными.

Простым называется суждение, не содержащее логических связок, элементами которого являются понятия (например, «Все кролики не едят мясо»). Сложное суждение состоит из нескольких простых суждений, соединённых между собой логическими связками (например, «Он является хорошим педагогом и учится заочно»).

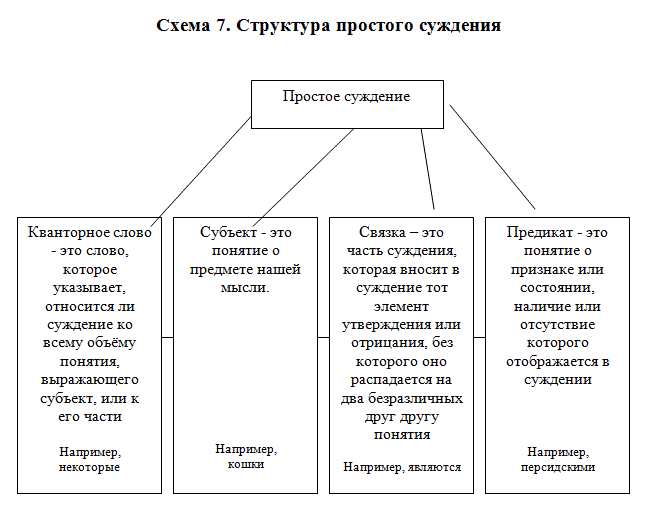
Простое суждение состоит из субъекта, предиката, связки, кванторного слова. Субъектом суждения называют понятие о предмете нашей мысли: о чём (о ком) мы мыслим, о чём мы судим? В приведённом выше примере в качестве субъекта выступает понятие «кролики». Предикатом суждения называют понятие о признаке или состоянии, наличие или отсутствие которого отображается в суждении: что мы приписываем предмету нашей мысли или что мы отрицаем у него? В приведённом выше примере предикатом является понятие «едят мясо». Субъект суждения принято обозначать буквой «S» (от лат. Subjectum), предикат – буквой «P» (от лат. Praedicatum), и в обобщённом виде логическая структура простого атрибутивного суждения может быть представлена как «S есть P» или «S не есть P». Связка в русском языке выражается словами «есть», «суть», «является» или их временными и модальными формами, иногда она заменяется тире, а часто и вовсе опускается, однако она всегда присутствует в суждении, ибо только связка вносит в суждение тот элемент утверждения или отрицания, без которого оно распадается на два безразличных друг другу понятия. Кванторное слово указывает, относится ли суждение ко всему объёму понятия, выражающего субъект, или к его части; кванторное слово выражается словами «все», или «ни один», или «некоторые» и другие.

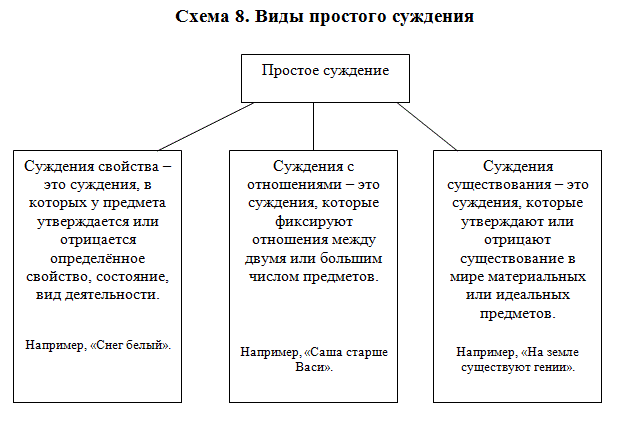
Простые суждения бывают трёх видов:

• суждения свойства (атрибутивные),
• суждения с отношениями,
• суждения существования (экзистенциальные).

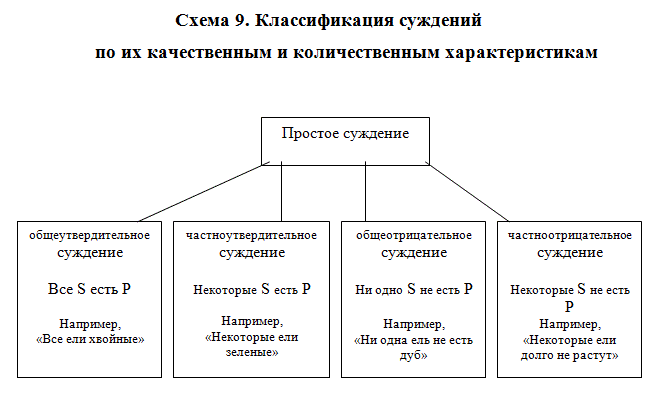
Суждения свойства (атрибутивные) – это суждения, в которых у предмета утверждается или отрицается определённое свойство, состояние, вид деятельности (например, «Мёд сладкий»). Суждения с отношениями – это суждения, которые фиксируют отношения между двумя или большим числом предметов (например, «Французский писатель Виктор Гюго родился позже французского писателя Стендаля»). Суждения существования (экзистенциальные) – это суждения, которые утверждают или отрицают существование в мире материальных или идеальных предметов (например, «Хомяки существуют»). В двузначной логике атрибутивные суждения иначе называются категорическими. Исходя из количественной и качественной характеристики суждений, получим классификацию суждений, в которой выделяются четыре типа суждений: общеутвердительное суждение, частноутвердительное суждение, общеотрицательное суждение, частноотрицательное суждение

• общеутвердительное суждение, структура которого «Все S есть P» («Все озёра – водоёмы»).
• частноутвердительное суждение, структура которого «Некоторые S есть P» («Некоторые спортсмены – чемпионы Олимпийских игр»).
• общеотрицательные суждения, его структура: «Ни одно S не есть P» («Ни один крокодил не является вегетарианцем»).
• частноотрицательное суждение, структура которого «Некоторые S не есть P» («Некоторые студенты не являются отличниками»).

Сложное суждение.
верх

Лекция 6: Сложное суждение.

Сложное суждение состоит из нескольких простых суждений, соединённых между собой логическими связками (например, «Он является хорошим педагогом и учится заочно»).

Логические связки представляют собой формальные аналоги союзов естественного языка.

Наиболее употребительными логическими связками являются конъюнкция, дизъюнкция, импликация, эквивалентность, отрицание.

Конъюнкции в естественном языке соответствуют союзы «и», «но», «а», «однако» и т.п. Это так называемые соединительные суждения (например, «В корзине у деда лежали подберёзовики и маслята»).

Дизъюнкции в естественном языке соответствуют союз «или», «либо» (например, «Иванов является юристом или Иванов является спортсменом»). Дизъюнкция бывает строгой и нестрогой. Строгая дизъюнкция – это логическая связка, включенная в сложное суждение, члены которого исключают друг друга, то есть не могут быть одновременно истинными (например, «Завтра я поеду в Москву на поезде или полечу на самолете»). Нестрогая дизъюнкция – это логическая связка, включенная в состав сложного суждения, члены которого не исключают друг друга, то есть могут быть истинными одновременно (например, «В магазине я покупаю хлеб или молоко»). Импликации в естественном языке соответствует союз «если…, то», который в повседневном языке обычно соединяет предложения, выражающие причинно-следственную связь явлений (например, «Если идёт дождь, то крыши домов мокрые»). Эквивалентное суждение – это суждение, в котором утверждается взаимная обусловленность двух ситуаций. Данное суждение выражается, как правило, посредством предложений с союзами «если и только если…, то», «тогда и только тогда…, когда» (например, «Если и только если солнце находится в зените, то тени от него являются самими короткими»). Отрицанию в естественном языке соответствует выражение «Неверно, что…» (например, «Неверно, что Земля – шар»). Чтобы понять истинно сложное суждение или ложно необходимо обратиться к таблице истинности.

Таблица истинности для конъюнкции имеет следующий вид:

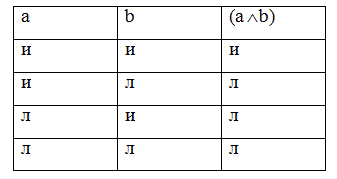
Таблица истинности нестрогой дизъюнкции имеет следующий вид:

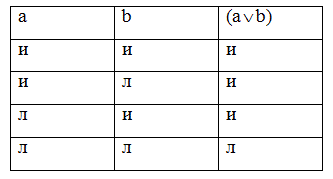
Таблица истинности строгой дизъюнкции представляет собой следующее:

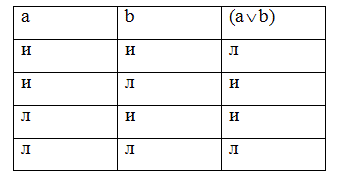
Таблица истинности импликации следующая:

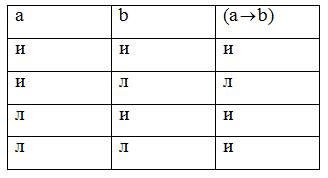
Таблица истинности эквивалентности имеет следующий вид:

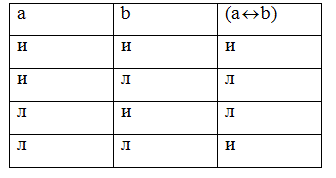
Логические законы.
верх

Лекция 7:Логические законы .

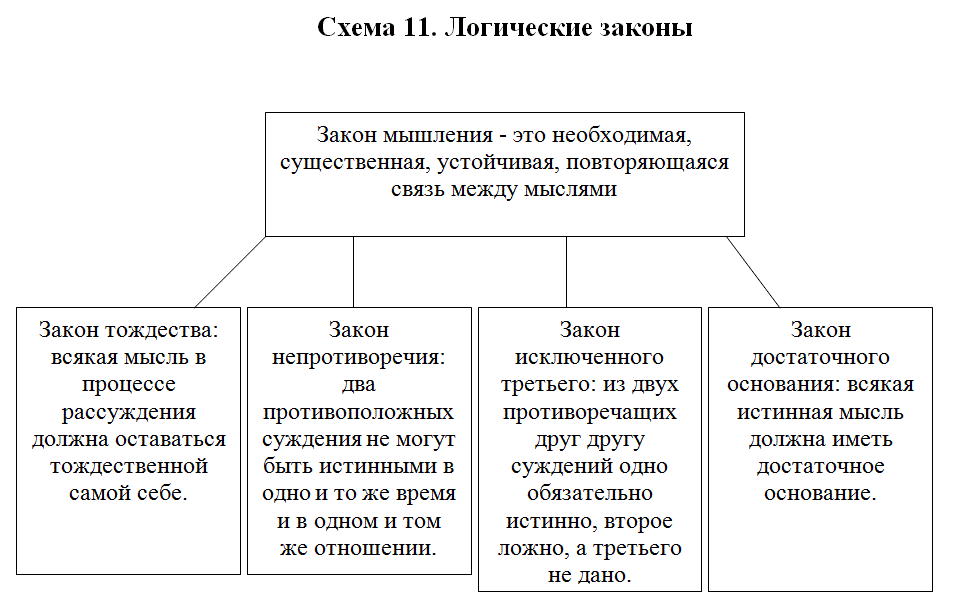
Закон мышления – это необходимая, существенная, устойчивая, повторяющаяся связь между мыслями. Наиболее простые и необходимые связи между мыслями выражаются в формально-логических законах. К основным формально-логическим законам относятся законы тождества, непротиворечия, исключённого третьего, достаточного основания. Первые три закона были выявлены и сформулированы Аристотелем.

• Закон достаточного основания был сформулирован в XVIII в. немецким философом Лейбницем.
• Закон тождества: всякая мысль в процессе рассуждения должна оставаться тождественной самой себе.
• Закон непротиворечия: два противоположных суждения не могут быть истинными в одно и то же время и в одном и том же отношении.
• Закон исключённого третьего: из двух противоречащих друг другу суждений одно обязательно истинно, второе ложно, а третьего не дано.
• Закон достаточного основания: всякая истинная мысль должна иметь достаточное основание.

Умозаключение.
верх

Лекция 8. Умозаключение.

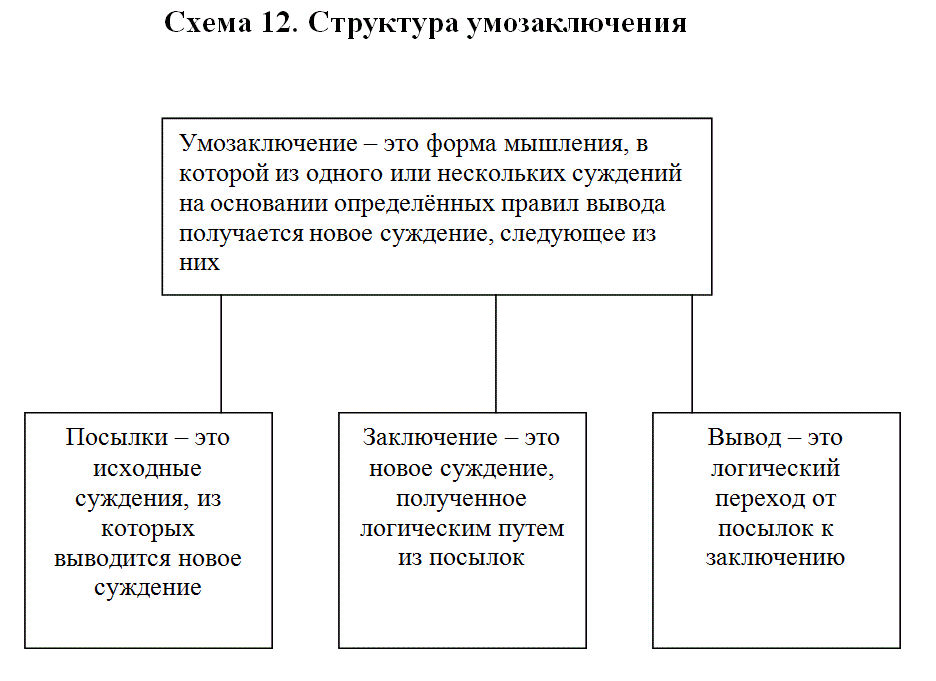
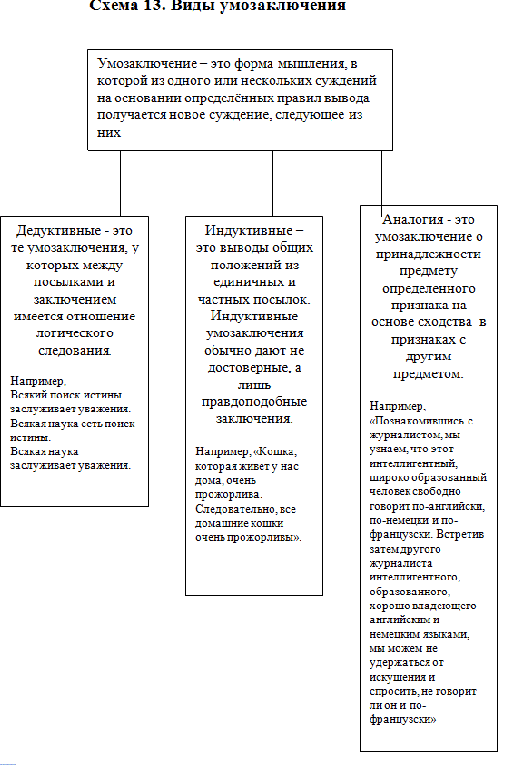
Умозаключение – это форма мышления, в которой из одного или нескольких суждений на основании определённых правил вывода получается новое суждение, следующее из них. Например, «Записка написана на японском языке или на китайском. Это не японский язык. Следовательно, записка написана на китайском языке». Структура всякого умозаключения включает посылки, заключение и логическую связь между посылками и заключением. Логический переход от посылок к заключению называется выводом. Умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии. Дедуктивные умозаключения – это умозаключения, у которых между посылками и заключением имеется отношение логического следования.

Например:

Все травоядные едят траву Лошадь травоядное животное Лошадь ест траву

Индуктивными умозаключениями называются выводы общих положений из единичных и частных посылок; индуктивные умозаключения обычно дают не достоверные, а лишь правдоподобные заключения.

Например,

«Учебник, который вы читаете, есть источник полезных знаний. Следовательно, все учебники являются источником полезных знаний».

Аналогия – это умозаключение о принадлежности предмету определенного признака на основе сходства в признаках с другим предметом.

Например,

«Студент экономического факультета Иванов отлично учился, прекрасно отработал производственную практику, активно участвовал в общественной жизни университета. Студент экономического факультета Петров отлично учился, прекрасно отработал производственную практику, активно участвовал в общественной жизни университета. Следовательно, если Иванов после окончания университета нашел престижную работу, то можно ожидать, что и Петров также найдет престижную работу».

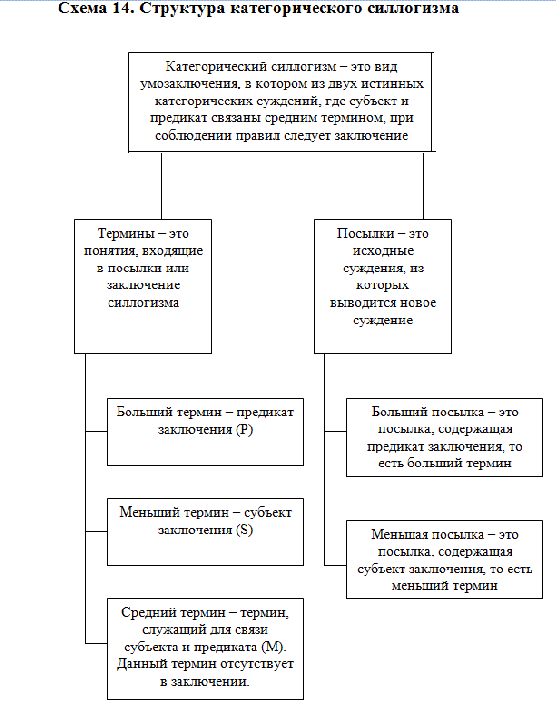
Категорический силлогизм – это вид дедуктивного умозаключения, в котором из двух истинных категорических суждений, где субъект и предикат связаны средним термином, при соблюдении правил следует заключение.

Например,

Все металлы электропроводны Медь есть металл Медь электропроводна

В составе категорического силлогизма имеются две посылки и заключение. Понятия, входящие в состав силлогизма, называются терминами силлогизма: больший термин, меньший термин, средний термин.

Термин, обозначающий субъект – это меньший термин (в приведенном выше примере это понятие «медь»). Термин, обозначающий предикат – больший термин (в приведенном выше примере это понятие «электропроводны»). Средний термин служит для связывания субъекта и предиката и отсутствует в заключении (в приведенном выше примере это понятие металл).

Посылка, содержащая предикат заключения, то есть больший термин, называется большей посылкой. Посылка, содержащая субъект заключения, то есть меньший термин, называется меньшей посылкой.

Силлогизм имеет четыре формы, фигуры, которые отличаются по положению среднего термина в посылках.

Силлогизм имеет четыре формы, фигуры, которые отличаются по положению среднего термина в посылках. Для того чтобы силлогизм был правильным, необходимо соблюдать особые правила фигур, правила посылок и правило терминов. Особые правила фигур

• I фигура. Большая посылка должна быть общей, меньшая утвердительной.
• II фигура. Большая посылка общая, одна из посылок, а также заключение отрицательные.
• III фигура. Меньшая посылка должна быть утвердительной, а заключение – частное.
• IV фигура. Общеутвердительных заключений не даёт.

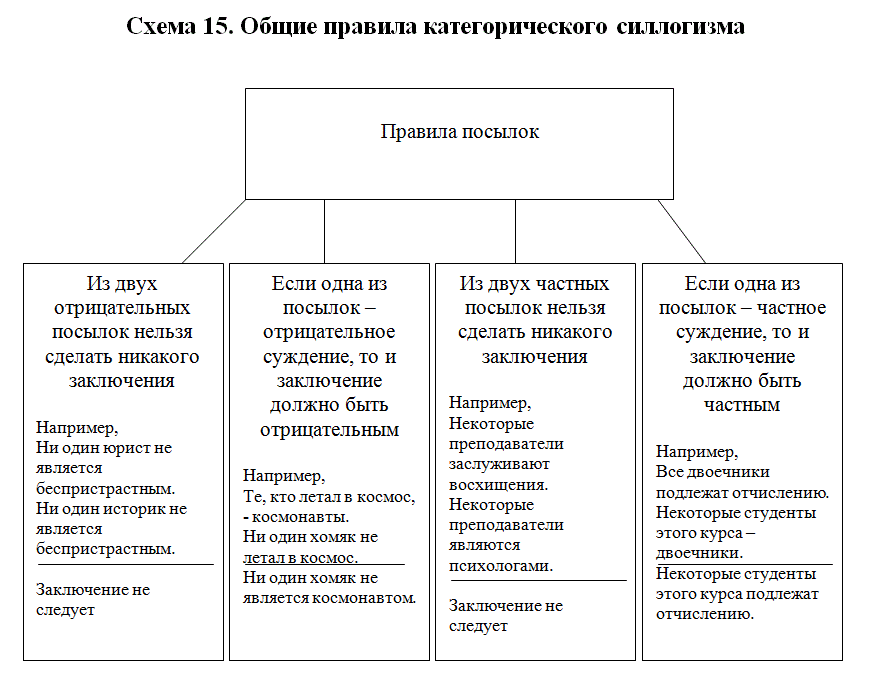
Правила посылок

1. Из двух отрицательных посылок нельзя сделать никакого заключения.
Например, Ярко-красные цветы не имеют запаха. Этот цветок не имеет запаха. Можно ли сделать вывод о том, что этот цветок ярко-красный? Нет, он может быть любого цвета.
2. Если одна из посылок отрицательная, то и заключение должно быть отрицательным.
3. Из двух частных посылок нельзя сделать заключение.
4. Если одна из посылок частная, то заключение должно быть частным.

Правило терминов

В силлогизме должно быть только три термина. Если появляется четвёртый термин, силлогизм разрушается, поскольку невозможно найти средний термина и сделать вывод.

В мышлении люди чаще используют сокращённый категорический силлогизм, называемый энтимемой. Энтимема – это силлогизм, в котором пропущена одна из посылок или заключение (например, «Все кашалоты – киты, следовательно, все кашалоты – млекопитающие»). При восстановлении энтимемы надо, во-первых, определить, какое суждение является посылкой, а какое – заключением. Посылка обычно стоит после союзов «так как», «потому что», «ибо» и т.п., а заключение стоит после слов «следовательно», «поэтому», «потому» и т.п.