Введение в математический анализ.
верх

Элементы теории множеств. Множество вещественных чисел. Понятие функций и способы их задания. Область определения функции и ее график. Основные элементарные функции и их графики. Сложные и обратные функции. Символика математической логики и ее использование. Последовательности. Предел функции. Предел последовательности. Бесконечно малые величины и их свойства. Бесконечно большие величины. Связь бесконечно больших и бесконечно малых. Основные теоремы о пределах функций. Первый и второй замечательные пределы. Сравнение бесконечно малых. Эквивалентные бесконечно малые и их использование при вычислении пределов. Определение непрерывности функции. Классификация точек разрыва функции. Непрерывность суммы, произведения и частного двух функций. Непрерывность сложной функции. Непрерывность элементарных функций. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.

Лекция 1: Понятие функции.

Переменная $х$ называется аргументом или независимой переменной, $у$ называют зависимой переменной или функцией. Эту зависимость сокращенно обозначают $у=f(x)$.

Множество всех значений, которые может принять зависимая переменная, называется областью значения функции и обозначается $E (f)$ или $E (y)$.

Чтобы наглядно представить поведение функции, строят ее график, рассматривая независимую переменную $х$ и функцию $у$ как прямоугольные координаты некоторой точки на плоскости $ 0_ху $ .

Основные функциональные зависимости.

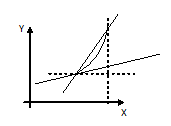
1. Прямая пропорциональная зависимость.

   Определение. Две переменные величины называются прямо пропорциональными, если при изменении одной из них в некотором отношении другая изменяется в том же отношении, т.е $у = кх$ , где $к$ есть коэффициент пропорциональности или угловой коэффициент, при этом $к = tg α$ (рис.1).

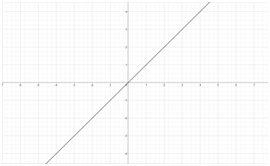
   Рис.1	Рис.2

2. Линейная зависимость.

   Определение. Две переменные величины $х$ и $у$ связаны линейной зависимостью, если

   $$ y=y_0+kx $$

   , где $к$ и $0$ – некоторые постоянные величины. В этом случае $ y_0 $ называют начальным отрезком (рис.2).

3. Обратная пропорциональная зависимость.

   Определение. Две переменные величины называются обратно пропорциональными, если при изменении одной из них в некотором отношении другая изменяется в обратном отношении.

   $$ \frac{k}{x}=y $$

   Если $к>0$, то график функции представляет собой равностороннюю гиперболу, расположенную в первом и в третьем квадрантах (рис.3).

   При $к<0$ график расположен во втором и в четвертом квадрантах.

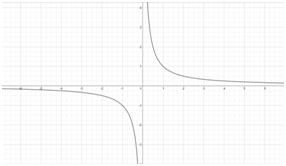
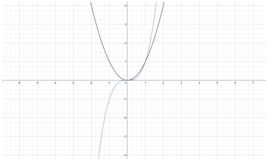
   Рис.3	Рис.4

    

4. Степенная функция.

   Здесь зависимость $у$ от $х$ выражается как:

   $$ y=x_n $$

   где $n$ = 0, 1, 2, 3 . . . Графики этих функций сходны с графиков квадратичной параболы

   $$ y=x^2 $$

   если $n$ – четное число, или с графиком параболы

   $$ y=x^3 $$

   если $n$ – нечетное число (рис.4).

5. Радикал.

   Эта зависимость записывается как

   $$ y= \sqrt[k]{x} $$

   где $n$ – натуральное число. Область определения функции $0 ≤ х < +∞ $ при $n$ – четном и $–∞ < х < +∞$ при $n$ – нечетном (рис.5).

6. Показательная функция.

   Аналитическое выражение для этой функции есть

   у = a^x

   , где $a$ называют основанием функции, а $х$ – показателем. Здесь $a$ – постоянное число, причем $a >0$ и $a ≠ 1$ . Эта функция определена при всех значениях $х$ , она имеет положительные значения и монотонно возрастает от 0 до +∞ при $ a >1$ и монотонно убывает от +∞ до 0 при $0 < a < 1$ (рис.6).

7. Логарифмическая функция.

   Аналитическое выражение для функции имеет вид $y = log^ax $ , где $a >0$ и $a ≠ 1$ . Область определения функции $0 < х < +∞ $ (рис.7).

   Рис.7

8. Тригонометрические функции.

   Аргументом тригонометрической функции является число, выраженное в радианах. Рассмотрим две наиболее важные функции.

   $ y= sin x $ и $y = cos x $

   Эти функции определены для всех значений $x$ . Они ограничены $| y | ≤ 1$ и имеют период $2π$ (рис.8).

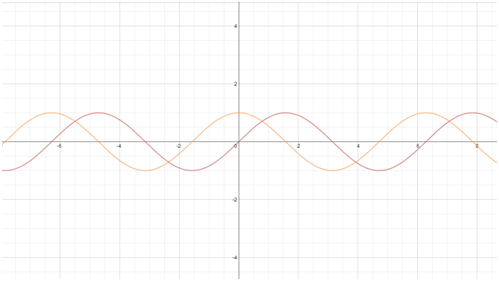
   Рис.8

    

9. Понятие обратной функции

   Пусть задана явная функция $у = f (x)$.

   Если из уравнения выразить $х$ через $y$ , а затем переименовать аргумент и функцию, то получим явное выражение для обратной функции.

   Пример.

   $$ у = х^2 – 2 у + 2 = х^2 х = \sqrt{y+2} у = \sqrt{y+2} $$

   Графики исходной и обратной функций симметричны относительно прямой $у = х$.

   Однако области определения исходной и обратной функций могут не совпадать. Так в рассмотренном примере область определения исходной функции составляет

   $ –∞ < х < +∞ $, а обратной функции $х ≥ –2$ .

   Из рассмотренных выше функций взаимно обратными будут показательная и логарифмическая функции при одинаковом основании.

Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.

Лекция 2: Предел функции.

Определение. Пусть $f (x)$ – функция, определенная на множестве $Х$ , и $а$ – предельная точка этого множества. Число $А$ называется пределом функции $f (x)$ при $х → а $ тогда и только тогда, когда для любого

$$ ε > 0 | f (x) – А | < ε $$

$$ lim f(x)= A $$

Если функция $f (x) = С $ постоянна в некоторой окрестности точки $а$ , то

$$ lim f (x) = С $$

Под последовательностью $x1, x2 , x3, . . ., x^n$ понимается функция $x^n = ∫(n)$, заданная на множестве натуральных чисел.

В бесконечно удаленной точке вводится понятие предела последовательности, то есть $x^n = а $, при $n → ∞$ , если для любого $ε > 0$ существует такое число $N$ , зависящее от $ε$ , что для всех натуральных $ n > N $ выполнено неравенство $| x^n – а | < ε $ .

Определение. Функция $ α( x ) $ называется бесконечно малой при $х → а$ или $х → ∞$ , если для любого $ε > 0 | α( x ) |< ε $ или $lim α( x ) = 0$ .

Алгебраическая сумма конечного числа бесконечно малых при $ х → а $ функций есть функция бесконечно малая при $х → а $.

Произведение ограниченной при $ х → а $ функции на бесконечно малую при $ х → а $ функцию есть функция бесконечно малая при $ х → а $.

Произведение конечного числа бесконечно малых при $ х → а $ функций есть функция бесконечно малая при $ х → а $.

Отношение двух бесконечно малых при $ х → а $ функций может быть функцией произвольного поведения при $ х → а $.

Основные свойства пределов.

1. Если каждое слагаемое алгебраической суммы конечного числа функций имеет предел при $ х → а $ , то предел суммы при $ х → а $ существует и равен алгебраической сумме пределов слагаемых. Пусть $ lim f (x) = А $ при $ х → а $ , $ lim g (x) = В $ при $ х → а $ , $ lim h (x) = С $ при $ х → а $ , тогда $ lim (f (x) + g (x) – h (x)) = А + В – С $ при $ х → а $.
2. Если каждый из сомножителей произведения конечного числа функций имеет предел при $ х → а $, то предел произведения при $ х → а $ , равен произведению пределов сомножителей. Пусть $ lim f (x) = А $ при $ х → а $ , и $ lim g (x) = В $ при $ х → а $ , тогда $ lim (f (x) ∙ g (x)) = lim f (x) ∙ lim g (x) = А∙В $ при $ х → а $
3. Постоянный множитель можно выносить за знак предела.
4. Если делимое $ f (x) $ и делитель $ g (x) $ имеют пределы при $ х → а $ и предел делителя отличен от нуля, то предел их частного при $ х → а $, равен частному пределов делимого и делителя. Пусть $lim f (x) = А$ при $х → а$ , и $lim g (x) = В$ при $х → а$ , тогда

   $$ lim\frac{f(x)}{g(x)}=\frac{A}{B} $$

   при $х → а$.

Замечательные пределы.

1. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице

   $$ lim\frac{sin x}{x}=1 $$

   при $х → 0$.
2. Рассмотрим последовательность число $e$ .

   $$ a_n=(1+\frac{1}{n})^n $$

   , где $n$ – натуральное число. Предел $a^n$ при

   $$ n → ∞ lim (1+\frac{1}{n})^n= e $$

   . Можно показать, что предел функции

   $$ ( 1 + \frac{1}{x}=y)^x = e $$

   при $ х → ∞$ . Заменим

   $$ \frac{1}{x}=y $$

   , тогда

   $$ ( 1 +\frac{1}{x}=y)^x=(1+y)^\frac{t}{γ} $$

   Поэтому

   $$ lim(1+y)^\frac{t}{γ}= e $$

   при $ у → 0 $ .

Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.

 

Лекция 3: Непрерывность функции.

 

Определение. Приращением некоторой переменной величины называется разность между новым значением этой величины и ее прежним значением.

Для обозначения приращения используется греческая буква $ ∆ $.

Например. $ ∆х = х – х^0 $ обозначает приращение величины $х $.

Пусть $ у = f (x) $ есть функция аргумента $х $ . Дадим аргументу $ х $ приращение $∆х$; тогда у получит приращение $∆у$ $ ∆у = f ( x+∆х ) – f (x)$ .

Пример. Оценить приращение аргумента $х$ и приращение функции $ y = x^3 $ , если $х$ изменился от –1 до 2.

Очевидно, что $ ∆х = 2 – (–1) = 3 $ и $ ∆у = 2^3 – (–1)^3 = 9 $ .

Определение. Функция $ f (x) $ , определенная на множестве $ Х $ , называется непрерывной при $ х → х_0$ , если:

функция определена при $ х = х_0 $ ;

приращение функции в точке $ х_0$ стремится к нулю, когда приращение аргумента $ ∆х → 0 $ , т.е.

$$ lim ( f (x_0+∆х)- f(x_0))=0 $$

при $ ∆х → 0 $ .

Определение. Точка $ х_0 $ , в которой нарушается непрерывность функции, называется точкой разрыва функции.

Здесь возможны два случая:

1. функция $f (x)$ определена при $ х = х_0 $ , причем

   $$ ∆у = f ( x_0+ ∆х )-f(x_0) $$

   не стремится к нулю при $ ∆х → 0 $ .
2. функция $ f (x) $ не определена при $ х = х_0 $ , и говорить о приращении функции в точке $ х_0 $ не имеет смысла. Классификация точек разрыва.

Точка $ х_0 $ функции $ f (x) $ называется точкой разрыва первого рода, если существуют конечные односторонние пределы функции.

$ А = f ( x_0 – 0) $ , $ В = f ( x_0 + 0) $

$ lim f (x) = f ( x_0 – 0) $ при $ х → х_0 – 0 $ ; $ lim f (x) = f ( x_0 + 0) $ при $ х → х_0+ 0 $ .

При этом функция $ f (x) $ не обязательно должна быть определена в точке $ x_0 $ , т.е. $ f (x_0) $ может не существовать.

Величина

$$ δ = f ( x_0 + 0) – f ( x_0 – 0) $$

называется скачком функции в точке $ x_0 $ .

Все прочие точки разрыва функции называются точками разрыва второго рода.

Пример. Функция

$$ f (x) =\frac{1}{x} $$

в точке $ х_0 = 0 $ терпит разрыв второго рода, так как при $ х → 0 – 0 f (x) → –∞ $ , при $ х → 0 + 0 f (x) → +∞ $ .

В этом случае прямая $ х = 0 $ называется вертикальной асимптотой.

Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.

 

Дифференциальное исчисление функций одной переменной.
верх

Определение производной функции. Геометрический и механический смысл производной. Уравнения касательной и нормали к кривой. Производная постоянной, суммы, произведения и частного двух функций. Производные тригонометрических функций. Производная показательной функции. Производная обратной функции. Производная логарифмической и обратных тригонометрических функций. Дифференцируемость функции. Дифференциал функции. Связь дифференциала с производной. Непрерывность дифференцируемой функции. Геометрический смысл дифференциала. Производная сложной функции. Логарифмическое дифференцирование. Производная степенной функции. Таблица производных. Производные высших порядков. Теоремы Ферма, Ролля, Лагранжа, Коши. Раскрытие неопределенностей и правило Лопиталя. Формула Тейлора.

Лекция 1: Определение производной функции.

 

Задача о скорости движения точки.

Пусть точка М движется по прямой Ох.

Каждому значению времени t соответствует определенное расстояние ОМ = х, то есть абсцисса х точки есть функция времени х = f( t ).

В момент времени t точка занимает положение М, а в момент t + ∆t она займет положение М', где ОМ' = х +∆х. Перемещение точки М за время ∆t будет

∆х = f( t+ ∆t ) – f( t ).

Отношение 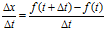выражает среднюю скорость изменения абсциссы х за промежуток времени ∆t. Предел средней скорости движения при стремлении ∆t к нулю называется мгновенной скоростью движения в момент t.

v = lim при ∆t → 0 или v = lim при ∆t → 0.

Полученное выражение представляет собой производную функции х по переменной t, то есть v = f '( t ) или v = х '( t ).

В этом состоит механический смысл производной.

Задача о касательной.

Пусть M( x,y ) – фиксированная точка непрерывной кривой. Рассмотрим другую точку М' ( х +∆х, y + ∆y ). Проведем секущую М М' до пересечения с осью 0х, с которой она образует угол φ. Определим угловой коэффициент секущей

к' = tg φ = .

Пусть точка М' стремится к точке М. Тогда ∆х устремится к нулю, и секущая устремится к предельному положению – касательной. При этом угол φ → a, а tg φ → tg a. Переходя к пределу при ∆х → 0 найдем угловой коэффициент касательной к = tg a = lim при ∆х → 0.

Этот предел называется производной функции y = f( x ) в точке х и обозначается lim = у' = f '( х ) при ∆х → 0.

В этом состоит геометрический смысл производной.(рис. 9)

Рис.9

 

Основные правила дифференцирования функций.

1. Производная постоянной величины равна нулю.
2. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же алгебраической сумме производных этих функций.
3. Производная произведения двух дифференцируемых функций равна произведению первого сомножителя на производную второго плюс произведение второго сомножителя на производную первого.
4. Производная частного двух дифференцируемых функций равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат исходного знаменателя.
5. Для дифференцируемой функции с производной не равной нулю, производная обратной функции равна обратной величине производной данной функции.

Таблицу производных можно найти в книге Шершнев В. Г. Математический анализ: учебное пособие, стр. 44-45.

Рекомендованная литература:

1. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
2. Шершнев В. Г. Математический анализ: сборник задач с решениями : учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2014. - 164 с.

 

Лекция 2: Дифференциал функции.

 

Пусть функция y = f(x) имеет производную в точке х:

Тогда можно записать: , где α→0, при .

Следовательно: Δy = f '(x)·Δ x+α·Δx .

Величина αΔx- бесконечно малая более высокого порядка, чем f'(x)Δx, т.е. f'(x)Δx, главная часть приращения Δу.

Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции. Обозначается dy или df(x).

dy = f'(x)Δx, или dy = f (x)dx

Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:

1) d(u ± v) = (u ± v)' dx = u' dx ± v' dx = du ± dv

2) d(uv) = (uv)' dx = (u' v + v' u)dx = vdu + udv

3) d(Cu) = Cdu

4)

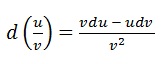
Пусть y = f(x), x = g(t), т.е у- сложная функция. Тогда dy = f' (x)g' (t)dt = f' (x)dx.

Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.

Однако, если х - независимая переменная, то dx = Δx, но если х зависит от t, то Δх≠dx. Таким образом форма записи dy = f '(x)Δx не является инвариантной.

Рекомендованная литература:

1. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
2. Шершнев В. Г. Математический анализ: сборник задач с решениями : учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2014. - 164 с.

 

3 Лекция: Производные и дифференциалы высших порядков.

 

Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную

y' = f '(x)

Если найти производную функции f'(x), получим вторую производную функции f(x).

y'' = f''(x), т.е. y'' = (y')'.

Этот процесс можно продолжить и далее, находя производные порядка n.

Также по формуле dⁿy = f ⁽ⁿ⁾(x)dxⁿ может быть найден дифференциал n- го порядка.

Рекомендованная литература:

1. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
2. Шершнев В. Г. Математический анализ: сборник задач с решениями : учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2014. - 164 с.

 

Лекция 4: Теоремы о производных.

 

Теорема Ролля. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка ɛ , a < ɛ < b, в которой производная функция f(x) равная нулю, f'(ɛ) = 0.

Теорема Лагранжа. Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка ɛ: a < ɛ < b, такая, что = f '(ɛ)

Теорема Коши. Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g'(x) ≠ 0 на интервале (a, b), то существует по крайней мере одна точка ɛ, a < ɛ < b, такая, что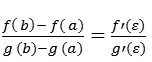

Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g''(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х → а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.

Теорема Тейлора. 1) Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно. Т.е. и все предыдущие до порядка n производные непрерывны и дифференцируемы в этой окрестности.

2) Пусть х- любое значение из этой окрестности, но х ≠ а. Тогда между точками х и а найдется такая точка ɛ, что справедлива формула:

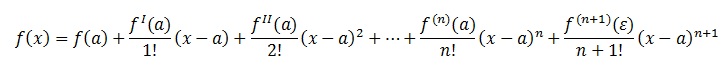
- это выражение называется формулой Тейлора.

Формулой Маклорена называется формула Тейлора при а = 0.

Рекомендованная литература:

1. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
2. Шершнев В. Г. Математический анализ: сборник задач с решениями : учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2014. - 164 с.

 

Применение дифференциального исчисления для исследования функций и построения их графиков.
верх

Условия возрастания и убывания функции. Локальный экстремум функции. Необходимые и достаточные условия локального экстремума. Отыскание наибольшего и наименьшего значений непрерывной на отрезке функции. Исследование на экстремум функции с помощью производных второго порядка. Исследование функций на выпуклость и вогнутость. Точки перегиба. Асимптоты кривых. Общая схема построения графиков функций

Лекция 1: Исследование функций с помощью производной.

Теорема. 1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f '(x) ≥0.

2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f (x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].

Аналогично можно сделать вывод о том, что если функция f(x) убывает на отрезке [a, b], то f' (x) ≤ 0 на этом отрезке. Если f' (x) < 0 в промежутке (а, b), то эта функция e,sdftn на отрезке [a, b].

Определение. Функция f(x) имеет в точке x₁ максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку x₁. Соответственно функция f(x) имеет в точке x₂ минимум, если f(x₂+ Δx) > f(x₂) при любом Δх ( Δх может быть и отрицательным).

Определение. Точки максимума и минимума функции называются точками экстремума. Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = x₁ и точка x₁ является точкой экстремума, то производная функции обращается в нуль в этой точке.

Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум.

Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.

Теорема. (Достаточные условия существования экстремума) Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку x₁, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки x₁). Если при переходе через точку x₁ слева направо производная функции f'(x) меняет знак с "+" на "-", то в точке х = x₁ функция f(x) имеет максимум, а если производная меняет знак с "-" на "+"- то функция имеет минимум.

На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:

1. Найти критические точки функции.
2. Найти значения функции в критических точках.
3. Найти значения функции на концах отрезка.
4. Выбрать среди полученных значений наибольшее и наименьшее.

Теорема. Пусть в точке х = x₁ f'(x₁) = 0 и f''(x₁) существует и непрерывна в некоторой окрестности точки x₁, тогда функция f(x) в точке х = x₁ имеет максимум, если f''(x₁)<0 и минимум, если f''(x₁)>0.

Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая обращена выпуклостью вниз на интервале (а, b), если все ее точки лежат выше любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.

Теорема. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла). Если f''(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).

Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная пересекает кривую.

Теорема. Пусть кривая определяется уравнением y=f(x). Если вторая производная f''(a) =0 или f''(a) не существует и при переходе через точку х=а f''(x) меняет знак, то точка кривой с абсциссой х=а является точкой перегиба.

Определение. Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.

Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть вертикальные и наклонные(частный случай – горизонтальные). Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 76-77)

Общая схема исследования функций.

1. Область существования функции. Это понятие включает в себя и область значений и область определения функции.
2. Точки разрыва. (Если они имеются).
3. Интервалы возрастания и убывания.
4. Точки максимума и минимума.
5. Максимальное и минимальное значение функции на ее области определения.
6. Области выпуклости и вогнутости.
7. Точки перегиба.(Если они имеются).
8. Асимптоты.(Если они имеются).
9. Построение графика.

Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
3. Математический анализ: Учебное пособие / В.Г. Шершнев. - М.: НИЦ ИНФРА-М, 2014. - 288 с.: 60x90 1/16. - (Высшее образование: Бакалавриат). (переплет) ISBN 978-5-16-005488-9, 500 экз.

Функции нескольких переменных.
верх

Функции нескольких переменных. Геометрический смысл функции двух переменных. Область определения. Предел функции. Непрерывность. Частные производные. Дифференцируемость функции. Полный дифференциал. Уравнения касательной плоскости и нормали к поверхности. Частные производные высших порядков. Экстремумы функции двух переменных. Необходимые и достаточные условия. Условный экстремум. Классические методы оптимизации. Функции нескольких переменных в экономической теории. Функции спроса и предложения. Функция полезности. Кривые безразличия.

Лекция 1: Функции нескольких переменных.

 

Пусть {M(x₁,..., x_m)} — множество точек пространства Rm и пусть каждой точке M из этого множества поставлено в соответствие некоторое число u. Тогда говорят, что на множестве {M} определена функция m переменных.

Обозначения: u = f(x₁,..., x_m) или u = f(M).

Множество {M} называется областью определения функции, а координаты x₁,..., x_m — независимыми переменными (или аргументами функции). Множество значений функции будем обозначать {u}.

В случае функции двух переменных будем использовать обозначения u = f(x, y) или z = f(x, y). График функции двух переменных z = f(x, y) — поверхность в прямоугольной системе координат Oxyz, точки которой имеют координаты (x, y, f(x, y)).

Разность  f (x+Dx, y) – f (x, y) называется частным приращением функции f (x, y) по переменной x.

Разность  f (x, y+Dy) – f (x, y) называется частным приращением функции f (x, y) по переменной y.

Определение. Если существует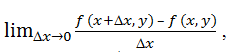

то он называется частной производной (первого порядка) функции z = f (x, y) по переменной x и обозначается

z_x' = = f_x'(x,y).

Определение. Если существует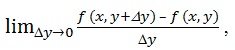

то он называется частной производной (первого порядка) функции z = f (x, y) по переменной y и обозначается

z_y' = = f_y'(x,y)

Частной производной n-го порядка функции нескольких переменных называется частная производная первого порядка от частной производной (n-1)-го порядка той же функции. 

Теорема. Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности.

Полный дифференциал.(см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 92-94)

Определение. Говорят, что в точке P₀(x₀,y₀) функция f (x,y) имеет максимум, если существует такая окрестность этой точки, что для всех точек P(x,y) этой окрестности, отличных от P₀, выполнено неравенство f(P₀) >f(P)

Аналогично определяется минимум функции.

Минимум и максимум функции называются ее экстремумами.

Теорема (необходимое условие экстремума). В точке экстремума функции нескольких переменных каждая ее частная производная либо равна нулю, либо не существует.

Точки, в которых выполнены эти условия, называются критическими.

Теорема (достаточные условия экстремума). Пусть функция z=f(x,y) определена и имеет непрерывные частные производные до 3-го порядка в некоторой окрестности точки M₀(x₀,y₀), в которой z_x' = z_y' = 0. Если при этом в этой точке выполнено условие

Δ = z_xx'' · z_yy'' –(z_xe'')² > 0,

то точка M₀ является точкой экстремума функции, причем точкой максимума, если z_xx'' < 0, и точкой минимума, если z_xx'' > 0.

Если же в этой точке M₀ Δ = z_xx'' · z_yy'' –(z_xe'')² < 0 , то экстремума в M₀ нет.

В том случае, если в M₀ Δ = z_xx'' · z_yy'' –(z_xe'')² = 0, теорема ответа не дает.

Функции нескольких переменных в экономической теории. (см подробнее Красс М.С. Математика для экономического бакалавриата: Учебник. – М.: ИНФРА-М, 2011.- 472 с.)

 

Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
3. Математический анализ: Учебное пособие / В.Г. Шершнев. - М.: НИЦ ИНФРА-М, 2014. - 288 с.: 60x90 1/16. - (Высшее образование: Бакалавриат). (переплет) ISBN 978-5-16-005488-9, 500 экз.

Неопределенный интеграл.
верх

Первообразная. Неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов. Основные приемы интегрирования: замена переменной и интегрирование по частям. Интегралы от элементарных дробей. Интегрирование рациональных дробей. Интегрирование выражений, содержащих тригонометрические функции. Интегрирование некоторых иррациональных выражений.

Лекция 1: Неопределенный интеграл.

 

Интегральное исчисление решает следующую задачу: по данному дифференциалу, а следовательно, и производной неизвестной функции F(x), требуется определить эту функцию.

Общее выражение для всех первообразных данной непрерывной функции f( x ) называется неопределенным интегралом от функции или от дифференциального выражения f( x ) dx и обозначается символом ò f( x ) dx = F( x ) + С.

Основные свойства неопределенного интеграла.

1. Дифференциал неопределенного интеграла равен подинтегральному выражению, а производная неопределенного интеграла равна подинтегральной функции.
2. Отличный от нуля постоянный множитель можно выносить за знак неопределенного интеграла.
3. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме неопределенных интегралов от этих функций.

Таблицу простейших неопределенных интегралов можно найти в литературе Шершнев В. Г. Математический анализ: учебное пособие, стр. 129).

Основные методы интегрирования.

Для вычисления интеграла необходимо, если это возможно, пользуясь различными способами, привести его к табличному виду и найти искомый результат (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 130-152).

1. Метод разложения.

Если функцию можно записать в виде f( x ) = f₁( x ) + f₂( x ), то

ò f( x ) dx = ò f1( x ) dx + ò f₂( x ) dx.

2. Метод подстановки ( метод введения новой переменной).

Пусть функция f( x ) непрерывна на интервале (а; b) и x = φ( t ) непрерывно дифференцируема на интервале (a; β). На основании свойства независимости неопределенного интеграла от выбора аргумента, и учитывая, что dx = φ'( t ) dt получаем формулу замены переменной

ò f( x ) dx =ò f(φ(t)) φ'( t ) dt

3. Метод интегрирования по частям.

Пусть u и v – непрерывно дифференцируемые функции от х. На основании формулы дифференциала произведения имеем d( u∙v ) = udv – vdu. Отсюда

udv = d( u∙v ) – vdu. Интегрируя, получим ò udv = ò d( u∙v ) – ò vdu или

ò udv = u∙v – ò vdu.

Эта формула показывает, что интеграл ò udv приводится к интегралу ò vdu, который может оказаться более простым, чем исходный, или даже табличным.

Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
3. Математический анализ: Учебное пособие / В.Г. Шершнев. - М.: НИЦ ИНФРА-М, 2014. - 288 с.: 60x90 1/16. - (Высшее образование: Бакалавриат). (переплет) ISBN 978-5-16-005488-9, 500 экз.

Определенный интеграл.
верх

Задача, приводящая к понятию определенного интеграла. Определение определенного интеграла, как предела интегральных сумм. Условия существования определенного интеграла и его основные свойства. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле. Интегрирование по частям в определенном интеграле. Некоторые геометрические приложения определенного интеграла Несобственные интегралы.

 

 

Лекция 1:Определенный интеграл. (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 154-163, 172-178)

 

Под определенным интегралом от данной непрерывной функции f( x ) на данном отрезке [а; b] понимается соответствующее приращение ее первообразной, т.е.

f( x ) dx = F( b ) – F( a ) (Формула Ньютона – Лейбница).

Здесь числа а и b называются пределами интегрирования.

Определенный интеграл от непрерывной функции не зависит от выбора первообразной для подынтегральной функции.

Рассмотрим часть графика функции f( x ) на отрезке [а, b]. Определенный интеграл от непрерывной неотрицательной функции равен площади криволинейной трапеции с основаниями f( а ) и f( b ) и боковыми сторонами (b – a) и отрезком функции f( x ).

Несобственные интегралы. (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013, стр.163-172)

Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
3. Математический анализ: Учебное пособие / В.Г. Шершнев. - М.: НИЦ ИНФРА-М, 2014. - 288 с.: 60x90 1/16. - (Высшее образование: Бакалавриат). (переплет) ISBN 978-5-16-005488-9, 500 экз.

Дифференциальные уравнения первого порядка.
верх

Задачи, приводящие к дифференциальным уравнениям. Общие сведения об уравнениях. Дифференциальные уравнения первого порядка. Задача Коши. Формулировка теоремы существования и единственности решения задачи Коши. Уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли. Уравнения в полных дифференциалах.

Лекция 1: Дифференциальные уравнения первого порядка.

 

В математике и физике часто встречаются задачи, для решения которых требуется решить уравнение, содержащее не только неизвестную функцию и ее аргумент, но и производную неизвестной функции.

Уравнение вида F(x,y,y',y'',y''',…,y(ⁿ)) = 0,

связывающее независимую переменную x , искомую функцию y = y (x) и ее производные , называется обыкновенным дифференциальным уравнением. Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.

Функция y =ϕ (x ) называется решением дифференциального уравнения на интервале (a;b), если при ее подстановке в это уравнение получается тождество, справедливое для всех x из интервала (a;b).

В общем случае дифференциальное уравнение первого порядка имеет вид F(x,y,y′) = 0),

где x – независимая переменная, y – неизвестная искомая функция, F – заданная функция трех переменных/

Дифференциальное уравнение первого порядка, которое можно записать в виде y′ = f(x,y) называется уравнением первого порядка, разрешенным относительно производной.

ТЕОРЕМА (Коши). Пусть в уравнении y′ = f(x,y) функция f(x y), удовлетворяет двум условиям:

1. f (x y), непрерывна в некоторой области D плоскости xOy;
2. ее частная производная fy′ (x,y) в области D ограничена.

Тогда для любой точки M0(x0,y0)∈ D существует единственное решение y = ϕ (x) уравнения y′ = f(x,y), определенное в некотором интервале (a,b),, содержащем точку x₀ , и удовлетворяющее условию y0 = ϕ(x0) .

Числа x0, y0 называются начальными значениями (данными) для решения ) y = ϕ(x) , а условие y0 = ϕ(x0) – начальным условием решения. Задача нахождения решения y =ϕ (x) дифференциального уравнения y′ = f(x,y), удовлетворяющего начальному условию y0 = ϕ(x0) , называется задачей Коши.

Определение. Общим решением дифференциального уравнения y′ = f(x,y) в области D существования и единственности решения задачи Коши называется функция y = ϕ( x, C) зависящая от x и одной произвольной постоянной C, которая удовлетворяет следующим двум условиям:

1. при любом допустимом значении постоянной С она удовлетворяет уравнению F(x,y,y′) = 0);
2. каково бы ни было начальное условие y₀ = ϕ(x0), где (x₀,y₀)∈ D , можно найти единственное значение C₀ такое, что функция y = ϕ (x,C₀) удовлетворяет данному начальному условию.

Уравнение Φ(x,y,C₀) = 0 , задающее общее решение в неявном виде, называется общим интегралом уравнения.

Уравнения с разделяющимися переменными: y' = f(x)·g(y) или f1(x)·g1(y)dx + f2(x)·g2(y)dy = 0 (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 200-203).

Однородные уравнения (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 203-206).

Линейные уравнения первого порядка. (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 207-210).

Уравнения Бернулли. (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 211-212).

Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
3. Математический анализ: Учебное пособие / В.Г. Шершнев. - М.: НИЦ ИНФРА-М, 2014. - 288 с.: 60x90 1/16. - (Высшее образование: Бакалавриат). (переплет) ISBN 978-5-16-005488-9, 500 экз.

Дифференциальные уравнения высших порядков.
верх

Дифференциальные 4уравнения второго порядка, допускающие понижение порядка. Линейные дифференциальные уравнения высших порядков. Линейная зависимость и линейная независимость функций на отрезке. Определитель Вронского и его свойства. Структура общего решения линейного однородного уравнения и линейного неоднородного уравнения. Решение линейных уравнений методом вариации произвольных постоянных. Линейные дифференциальные уравнения с постоянными коэффициентами. Решение линейного однородного дифференциального уравнения с постоянными коэффициентами. Характеристическое уравнение. Отыскание частного решения линейного неоднородного уравнения с постоянными коэффициентами методом подбора по виду правой части.

Лекция 1: Дифференциальные уравнения высших порядков.

Уравнения, содержащие только x и y(ⁿ ): y(ⁿ ) = f(x) (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 215-216).

Общее решение такого уравнения получается в результате - кратного последовательного интегрирования правой части уравнения.

Уравнения, не содержащие искомой функции и ее производных до порядка (k – 1) включительно, т. е. не содержит искомой функции и ее производных до порядка ( k −1) включительно. (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 216-217)

Это уравнение допускает понижение порядка на k единиц заменой y(^k ) = p(^x ).

Уравнения, не содержащие независимого переменного. (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 217-218)

Порядок такого уравнения можно понизить на единицу заменой p = y′, причем p рассматривается как новая неизвестная функция, аргументом которой является y, т. е. p = p( y).

Линейные однородные уравнения второго порядка с постоянными коэффициентами:

y'' + py' + qy = 0, где p и q некоторые действительные числа.

λ² +pλ +q = 0 - характеристическое уравнение для уравнения y'' + py' + qy = 0.

Корни характеристического уравнения называются характеристическими корнями уравнения.

Характеристическое уравнение есть алгебраическое уравнение 2-й степени. В алгебре доказывается, что такое уравнение имеет 2 корня, которые могут быть как действительные, так и комплексные числа (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 221-225). Доказывается также, что комплексные корни такого уравнения попарно сопряжены.

Решение линейного однородного уравнения второго порядка с постоянными коэффициентами зависит от того, какими числами являются корни характеристического уравнения (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 228-230)

Линейные неоднородные уравнения второго порядка с постоянными коэффициентами (см. подробнее Шершнев В. Г. Математический анализ: учебное пособие, стр. 231-234).

 

Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
3. Математический анализ: Учебное пособие / В.Г. Шершнев. - М.: НИЦ ИНФРА-М, 2014. - 288 с.: 60x90 1/16. - (Высшее образование: Бакалавриат). (переплет) ISBN 978-5-16-005488-9, 500 экз.

Числовые ряды.
верх

Числовой ряд. Сумма ряда. Свойства сходящихся рядов. Необходимое условие сходимости ряда. Признаки сходимости знакоположительных рядов: признаки сравнения, признак Даламбера, радикальный и интегральный признаки Коши. Знакопеременные ряды. Абсолютная и условная сходимости. Теорема Лейбница.

Определение. Сумма членов бесконечной числовой последовательности a₁ , a₂,…, a_n,… называется числовым рядом и обозначается a₁ + a₂ +…+ a_n+ … =

a_n – общий член ряда, n-й член ряда

S_k – k-я частичная сумма ряда

Числовой ряд сходится,если существует

Число S называется суммой ряда:



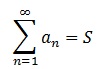
Числовой ряд расходится,если не существует

Свойства числовых рядов



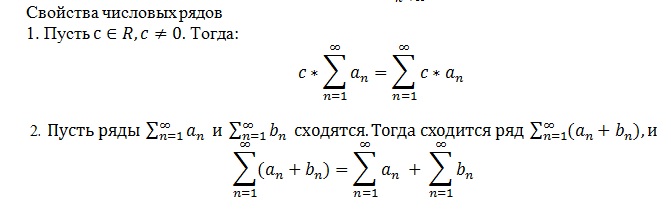
Теорема (необходимый признак сходимости ряда):



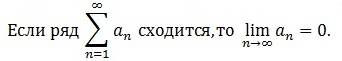
Знакопостоянные ряды.

Если для любого n a_n≤0 или a_n≥0,то ряд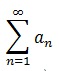 называется знакопостоянным.

Теорема (признак сравнения, признак Вейерштрасса):



Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
3. Математический анализ: Учебное пособие / В.Г. Шершнев. - М.: НИЦ ИНФРА-М, 2014. - 288 с.: 60x90 1/16. - (Высшее образование: Бакалавриат). (переплет) ISBN 978-5-16-005488-9, 500 экз.

Функциональные ряды. Степенные ряды.
верх

Степенные ряды. Теорема Абеля. Радиус и интервал сходимости степенного ряда. Свойства степенных рядов. Почленное дифференцирование и интегрирование степенных рядов. Разложение функций в ряды Тейлора и Маклорена. Применение рядов к приближенным вычислениям.

Лекция 1: Функциональные ряды. Степенные ряды.

Определение. Если членами ряда будут не числа, а функции от х, то ряд называется функциональным.

Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях переменной х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной х, при которых ряд сходится.

Совокупность таких значений называется областью сходимости (см подробнее Шершнев В. Г. Математический анализ: учебное пособие , стр. 257-258).

Определение:

Функциональный ряд вида 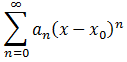называется степенным

рядом с центром разложения в точке x ₒ ,

а числа называется коэффициентами степенного ряда.

Замечание:

Сделаем замену переменной:

Тогда степенной ряд будет выглядит так: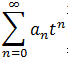

Для исследования на сходимость степенных рядов удобно использовать признак Даламбера. (см подробнее Шершнев В. Г. Математический анализ: учебное пособие , стр. 258-264).

Разложение функций в степенные ряды.

Разложение функций в степенной ряд имеет большое значение для решения различных задач исследования функций, дифференцирования, интегрирования, решения дифференциальных уравнений, вычисления пределов, вычисления приближенных значений функции.

Возможны различные способы разложения функции в степенной ряд. Такие способы как разложение при помощи рядов Тейлора и Маклорена были рассмотрены ранее. (См. Формула Тейлора).

Применение формулы Тейлора для разложения функций в степенной ряд широко используется и имеет огромное значение при проведении различных математических расчетов. Непосредственное вычисление интегралов некоторых функций может быть сопряжено со значительными трудностями, а замена функции степенным рядом позволяет значительно упростить задачу. Нахождение значений тригонометрических, обратных тригонометрических, логарифмических функций также может быть сведено к нахождению значений соответствующих многочленов. Если при разложении в ряд взять достаточное количество слагаемых, то значение функции может быть найдено с любой наперед заданной точностью. Практически можно сказать, что для нахождения значения любой функции с разумной степенью точности (предполагается, что точность, превышающая 10 – 20 знаков после десятичной точки, необходима очень редко) достаточно 4-10 членов разложения в ряд.

Применение принципа разложения в ряд позволяет производить вычисления на ЭВМ в режиме реального времени, что немаловажно при решении конкретных технических задач. Разложение в ряд некоторых элементарных функций (см подробнее Шершнев В. Г. Математический анализ: учебное пособие , стр. 267-273).

Рекомендованная литература:

1. Туганбаев А. А. Математический анализ: Пределы / А. А. Туганбаев.– 2-е изд., стереот. - М. : Флинта, 2011, стр. 24-30
2. Шершнев В. Г. Математический анализ: учебное пособие / В.Г. Шершнев. - М. : НИЦ ИНФРА-М, 2013. - 288 с.
3. Математический анализ: Учебное пособие / В.Г. Шершнев. - М.: НИЦ ИНФРА-М, 2014. - 288 с.: 60x90 1/16. - (Высшее образование: Бакалавриат). (переплет) ISBN 978-5-16-005488-9, 500 экз.