Математические методы исследования операций Назад на образовательную программу
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ - МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ СТУДЕНТАМ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
Разделы
Список Литературы
- Балдин, К.В. Математические методы и модели в экономике : учебник / К.В. Балдин, В.Н. Башлыков, А.В. Рокосуев ; под ред. К.В. Балдин. - М. : Флинта, 2012. - 328 с. - читать в библиотеке
- Математические методы и модели исследования операций : учебник / под ред. В.А. Колемаев. - М. : Юнити-Дана, 2015. - 592 с. - читать в библиотеке
Дополнительная литература
- Андрейчиков, А.В. Анализ, синтез, планирование решений в экономике : учебник / А.В. Андрейчиков, О.Н. Андрейчикова. - 2-е изд., доп. и перераб. - М. : Финансы и статистика, 2004. - 467 с. - читать в библиотеке

Ваш библиотекарь |
Внимание!Для входа в Электронную Библиотеку Вам нужно получить Логин и Пароль.
|
 |
Форма контроля
Форма отправки результатов (ТЕСТ, РЕФЕРАТ)
|
|

ВАШ Куратор(495) 632-00-78 |
Содержание разделов печать раздела -
Линейное программирование
верх
Общая задача линейного программирования (ЛП) заключается в нахождении экстремума линейной целевой функции при наличии ограничений на переменные в виде линейных неравенств или уравнений на переменные и условий неотрицательности переменных. Линейное программирование нашло наибольшее распространение в экономике при принятии оптимальных решений. Любая оптимизационная экономико-математическая модель задачи ЛП включает в себя три основных части:
- Целевая функция, оптимум которой необходимо найти.
- Ограничения на переменные задачи в виде линейной системы неравенств (уравнений).
- Условия неотрицательности переменных.
В задачах ЛП некоторому набору значений переменных, который удовлетворяет ограничениям задачи, отвечают допустимые решения. А те из них, которые приводят к максимуму или минимуму целевой функции, определяют оптимальные решения. Большинство задач ЛП, которые имеют реальный смысл, определяются единственным оптимальным решением совместной системы ограничений. Если система ограничений несовместна, то задача вообще не имеет допустимых решений, а потому и оптимального решения.
$Z=p_1x_1+p_2x_2+...+p_nx_n>max$
при задании $m$ ограничений,которые состоят в общем случае из $r$ неравенств и $(m – r)$ уравнений
$a_{i1}x_1+a_{i2}x_2+...+a_{in}x_n≤b_i{i=1...r}$
$a_{k1}x_1+a_{k2}x_2+...+a_{kn}x_n≤b_k{k=r+1...m}$
и условий неотрицательности
$x_j≥0(j=1...n)$, $b_k≥0(k=r+1...m)$
Эти формулы составляют экономико-математическую модель основной задачи ЛП. Ограничения любой задачи ЛП являются системой неравенств (уравнений). А совокупность решений таких систем, при условии, что они совместимы, составляют выпуклые множества с конечным числом узловых точек (вершин). Когда в систему ограничений-неравенств входят только две переменные $х_1$ и $х_2$, это множество легко изобразить на плоскости в системе координат $х_1$ и $х_2$. При этом задачу можно решить графическим методом для двух переменных$х_1$ и $х_2$. Сформулируем алгоритм графического метода:
- построить многоугольник допустимых решений на основании заданной системы ограничений;
- найти вершины многоугольника как точки пересечения полуплоскостей ограничений;
- вершина, для которой целевая функция приобретает оптимальное значение (максимальное или минимальное), отвечает разыскиваемому решению;
- координаты этой вершины являются оптимальными значениями переменных.
При количестве переменных $n> 2$ задачу ЛП решают аналитическим методом, который называется симплекс-методом (1947г.). Алгоритм симплекс-метода основной задачи ЛП состоит из трёх частей:
- исключение 0-уравнений;
- нахождение опорного (допустимого базисного) решения;
- получение оптимального решения.
Далее решение задачи ЛП при условии неотрицательности переменных заключается в следующем.
- Исключение 0-уравнений. Каждая из $(m – r)$ ограничений-равенств (0-уравнений) является уравнением $(n – r)$ мерных плоскостей $n-мерного$ пространства. Процедура исключения 0-уравнений заключается в использовании модифицированных жордановых исключений с выбором разрешающего элемента для замены координатной плоскости $x_s = 0$ новой плоскостью, которая задаётся 0-уравнением. При этом зависимое 0-уравнение и независимая переменная $x_s$ меняются местами, и «0» перемещается наверх им
- Получение опорного решения. К поиску опорного решения приступают тогда, когда исключены все 0-уравнения и свободные члены в симплексной таблице будут $b_i$. Если 0-уравнений в исходной симплекс-таблице нет, то свободные члены будут иметь первоначальное обозначение $b_j$. Когда в задаче ЛП получено опорное решение, то этому отвечает случай неотрицательных свободных членов симплексной таблицы $b^/_i ≥ 0$.
- Получение оптимального решения. Если все коэффициенты строки целевой функции симплексной таблицы оказались положительными, то задача ЛП решена. В противоположном случае с помощью модифицированного жорданова исключения по выбранному разрешающему элементу знак у нового коэффициента оказывается положительным. Так поступают, пока в строке все коэффициенты не станут положительными (оптимальное решение получено).
С каждой основной задачей ЛП можно связать другую линейную задачу, которая называется двойственной. При этом первичная задача по отношению к своей двойственной называется прямой. Так, основной (прямой) задаче ЛП по максимизации целевой функции при наличии ограничений отвечает двойственная задача по минимизации целевой функции при выполнении соответствующих ограничений.
Транспортная задача
верх
Целью транспортной задачи является такое планирование перевозок груза от поставщиков к потребителям, чтобы обеспечить минимальные транспортные расходы. Введём обозначение: $x_{ij}$– переменные, которые подлежат определению и выражают количество груза, который перевозится от $i–го$ поставщика к $j–му$ потребителю $(i =1. . . m, j = 1. . .n)$; $c_{ij}$ – стоимость перевозки единицы груза от $i–го$ поставщика к $j–му$ потребителю; $а_i$– количество единиц груза у $i–го$ поставщика; $b_j$ – количество единиц груза, которое нужно $j–му$ потребителю. Рассмотрим наиболее распространённую постановку транспортной задачи по минимизации общей стоимости перевозок. В некоторых задачах практической деятельности может минимизироваться время перевозок, определяться кратчайшее расстояние при заданной сети дорог и др.
Пусть есть т поставщиков груза в количестве $а_1, а_2, . . . а_i, . . .a_m$ единиц и $n$ потребителей этого груза, потребность которых составляет $b_1, b_2, . . . , b_j, . . . , b_n$ единиц. Известны стоимости перевозок единицы груза от $i–го$поставщика к $j–му$ потребителю $c_{ij} (i =1. . . m, j = 1. . .n)$. Необходимо составить такой оптимальный план перевозок груза, который обеспечил бы минимальные транспортные расходы. Выходные данные задачи удобно представить в виде транспортной таблицы, строка которой отвечает поставщику, а столбец – потребителю:
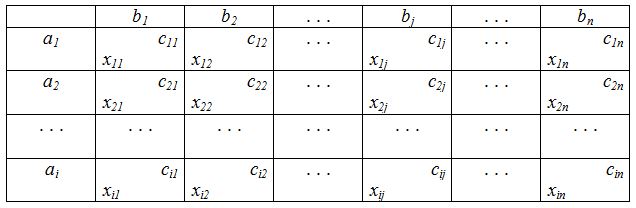
На практике при перевозке грузов может возникнуть одна из трёх ситуаций.:
- Количество единиц груза у поставщиков отвечает спросу со стороны потребителей, что отображается в условии баланса
- Количество груза у всех поставщиков больше спроса в грузах потребителей:
- Количество грузов у всех поставщиков меньше потребности в данном грузе всех потребителей. Поэтому каждый поставщик весь свой груз вывезет, а часть потребителей получит груза меньше необходимого количества; ограничение первой группы будут теми же.
$\sum_{i=1}^m a_i=\sum_{j=1}^n b_j$
Данная транспортная задача является сбалансированной, когда количество груза у поставщиков равняется спросу на грузы потребителей, а модель такой транспортной задачи – закрытой.
Поэтому часть груза у поставщиков останется, а потребители получают весь необходимый груз.
Транспортная задача связана с задачами ЛП, но ей присущи такие особенности:
- ограничения закрытой модели задаются в виде уравнений, а открытой модели – в виде смешанной системы ограничений – неравенств и уравнений, которые также могут быть возведены к ограничениям в виде уравнений;
- каждая неизвестная входит лишь в два уравнения;
- коэффициенты при неизвестных – единицы.
Для получения допустимого решения могут быть такие специальные методы, как метод северо-западного угла, метод минимального элемента, а для получения оптимального решения – метод потенциалов.
Метод северо-западного угла.
Определение переменных начинают с левой верхней клетки таблицы. Заполнение клеток происходит слева направо и сверху вниз. На последнем шаге процесса остаётся одна строка и один столбец. После заполнения клетки, которая находится на их пересечении, процесс завершается. Это означает, что весь груз или вывезен от поставщиков к потребителю, или у поставщиков остаётся часть груза.
Метод минимального элемента.
В предыдущем методе совершенно не учитываются транспортные расходы. Это приводит к увеличению количества шагов. В методе минимального элемента при построении базисного решения такой недостаток устранён. Определение объёма перевозок начинается с клетки, которая имеет минимальную стоимость перевозок. Как и в методе северо-западного угла, соответствующая строка или столбец исключаются из последующего рассмотрения, а потребность потребителя или наличие груза у поставщика уменьшается на выбранную величину. На последнем шаге остаются одна строка и один столбец. После заполнения клетки, которая стоит на их пересечении, процесс завершается.
Метод потенциалов.
Это один из наиболее эффективных методов нахождения оптимального плана транспортной задачи. Поставим в соответствие каждому поставщику некоторое число $U_i$, а потребителю – число $V_j$ . Эти числа называются соответственно потенциалом поставщика и потенциалом потребителя. Для базисных перевозок $U_i + V_j = C_{ij}$. Для небазисных перевозок введём обозначение $U_i + V_j = C'_{ij}$. Тогда условия оптимума допустимого базисного решения запишется виде:
- для базисных перевозок:$Δ_{ij} =С'_{ij} – C_{ij} = 0$;
- для небазисных перевозок (пустых клеток): $Δ_{ij} =С'_{ij} – C_{ij} ≤ 0$.
Для оптимума допустимого базисного решения необходима и достаточна его потенциальность. Для правильного перемещения перевозок строится цикл. Под циклом понимают замкнутый путь, который соединяет незаполненную клетку с ней же самой и который проходит через заполненные клетки. Метод потенциалов обеспечивает монотонное уменьшение значения целевой функции и позволяет по конечному числу шагов найти её минимум.
Системы массового обслуживания
верх
При исследовании многих сложных систем, связанных с различными сферами человеческой деятельности, часто приходится сталкиваться с системами, предназначенными для решения однотипных задач. Примерами таких систем являются автозаправочные станции (АЗС), предприятия сферы обслуживания, торговые организации. Каждая система состоит из определенного числа обслуживающих единиц, называемых каналами обслуживания. Каждый канал предназначен для определенных заявок. В качестве заявок выступают автомашины, клиенты в мастерских сферы обслуживания и поликлиниках, покупатели и т.д. Поступающие на обслуживание заявки образуют поток заявок.
Многие из исследуемых систем массового обслуживания (СМО) представляют собой не одну СМО, а цепочку связанных между собой входящими и выходящими потоками заявок СМО, каждая из которых называется фазой обслуживания. В общем случае и время прихода заявок в систему, и продолжительность их обслуживания являются случайными величинами, поэтому к моменту прихода очередной заявки не всегда имеется в наличии свободный канал. В этом случае заявка встает в очередь на обслуживание. Предметом теории массового обслуживания является построение математических моделей зависимости показателей эффективности СМО от заданных условий её функционирования. В качестве показателей эффективности используются:
- средние величины числа заявок, обслуженных в единицу времени; числа заявок в очереди; времён ожидания в очереди и пребывания в системе и т.д.;
- вероятности обслуживания без ожидания; обслуживания в полном объёме; простоя каналов и т.д.
Классификация СМО.
По характеру поступления заявок:
- системы с регулярным потоком заявок, когда интенсивность потока или постоянна, или является заданной функцией времени;
- системы со случайным потоком заявок, когда задана функция распределения вероятности поступления заявок в систему.
По количеству одновременно поступивших заявок:
- системы с ординарными потоками заявок;
- системы с неординарными потоками заявок.
По характеру обслуживания заявок:
- системы с отказом;
- системы с ограниченным ожиданием;
- системы с ожиданием без ограничений.
По числу каналов обслуживания:
- системы одноканальные;
- системы многоканальные.
Все реально функционирующие системы разделяются на два класса:
- системы, которые относятся к специальному классу случайных процессов – гибели и размножения. Особенностью таких систем является постоянство потока входящих заявок и их обслуживание;
- системы, для которых невозможно получить точноеаналитическое решение задач анализа и синтеза. Здесь наибольшие успехи достигнуты в результате использования методов математической статистики.
Потоки событий.
Процесс работы любой СМО представляет собой случайный процесс, когда изменение её состояния происходит в соответствии с вероятностными характеристиками. Для описания процессов широко применяется математический аппарат марковских случайных процессов. Переход системы из состояния в состояние происходит под воздействием каких-то потоков событий с интенсивностью $λ$. Простейший поток обладает следующими свойствами:
- Стационаорность.
- Ординарность, то есть события в потоке происходят поодиночке.
- Отсутствие последействия, то есть события появляются в последовательный момент времени независимо друг от друга.
Геометрической интерпретацией описанных процессов являются так называемые графы состояний. Пусть имеем два пункта. Введём обозначения для дискретных состояний: $S_0$– оба пункта свободны; $S_1$ – первый занят, второй свободен; $S_2$ – первый свободен, второй занят; $S_3$ – оба заняты. Очевидно, что сумма вероятностей пребывания системы в одном из четырёх состояний в любой момент времени равна единице. Будем рассматривать плотности вероятности перехода $λ$ как интенсивности потоков событий, переводящих систему из состояния в состояние. По графу состояний можно составить дифференциальное уравнение Колмогорова для определения вероятности состояния системы как функции времени. На основании этих уравнений можно получить систему линейных алгебраических уравнений. Среди многообразия случайных процессов можно выделить так называемый процесс гибели и размножения, для которого граф состояний представляет собой последовательную цепочку состояний, где переходы могут осуществляться только в соседние состояния. Для состояния $S_0$ имеем:$P_0λ_{01} = P_1λ_{10}$. Для состояния $S_1$ имеем: $P_1λ_{12} = P_2λ_{21}$ и так далее.
Одноканальная СМО с отказами.
В системе имеется один канал, на который поступает поток заявок с интенсивностью $λ$, а обслуживание происходит с интенсивностью μ, и система может находиться только в одном из двух состояний: $S_0$ – канал свободен и $S_1$ – канал занят. Такой системе соответствуют условия: $P_0λ = P_1μ$ ; $P_0 + P_1 = 1$, из которой находят предельные вероятности состояний, определяющие относительную пропускную способность системы и вероятность отказа.
Многоканальная СМО с отказами.
В зависимости от числа занятых каналов можно выделить следующее состояние системы:
- $S_0$ – все каналы свободны;
- $S_1$ – занят только один канал;
- $S_n$ – занятывсе $n$ каналов.
Зная предельную вероятность начального состояния и все вероятности состояний, можно найти характеристики эффективности многоканальной СМО с отказами: вероятность отказа, относительную пропускную способность, абсолютную пропускную способность, среднее число занятых каналов.
Одноканальная СМО с неограниченной очередью.
Для такой системы характерен процесс гибели и размножения, но с бесконечным числом состояний.Эти состояния можно обозначить следующим образом: $S_0$ – канал свободен; $S_1$ – канал занят, обслуживается одна заявка и очереди нет; $S_2$ – канал занят и одна заявка стоит в очереди; $S_k$ – канал занят, и $k$ – 1 заявок стоят в очереди и т.д. Оценить эффективность функционирования такой системы можно, используя следующие характеристики:
- Относительная пропускная способность: $Q = 1$, поскольку при отсутствии ограничений на длину очереди каждая заявка, пришедшая в систему, будет обслужена.
- Абсолютная пропускная способность: $A = Qλ = λ$.
- Среднее число заявок в системе определяется по обычным формулам математического ожидания.
Сетевое планирование и управление
верх
Сетевое планирование – это метод планирования работ, операции в которых, как правило, не повторяются. Для проведения сетевого планирования вначале необходимо расчленить проект на ряд отдельных работ и составить логическую схему (сетевой граф). Работа – это любые действия, сопровождающиеся затратами ресурсов или времени и приводящие к определённым результатам. На сетевых графах работы обозначаются стрелками. Для указания того, что одна работа не может выполняться раньше другой, вводят фиктивные работы, которые изображаются пунктирными стрелками. Продолжительность фиктивной работы принимается равной нулю. Событие – это факт окончания всех входящих в него работ. Считается, что оно происходит мгновенно. На сетевом графе событие изображается в виде вершин графа. Ни одна выходящая из данного события работа не может начаться до окончания всех работ, входящих в это событие. С исходного события (которое не имеет предшествующих работ) начинается выполнение проекта. Завершающим событием (которое не имеет последующих работ) заканчивается выполнение проекта. После построения сетевого графа необходимо оценить продолжительность выполнения каждой работы и выделить работы, которые определяют завершение проекта в целом. Нужно оценить потребность каждой работы в ресурсах и пересмотреть план с учётом обеспечения ресурсами. Правило построения сетевых графиков.
- Завершающее событие лишь одно.
- Исходное событие лишь одно.
- Любые два события должны быть непосредственно связаны не более чем одной работой-стрелкой. Если два события связаны более чем одной работой, рекомендуется ввести дополнительное событие и фиктивную работу.
- В сети не должно быть замкнутых циклов.
Метод критического пути.
Этот метод используется для управления проектами с фиксированным временем управления работ и позволяет ответить на следующие вопросы:
- Сколько времени потребуется на выполнение всего проекта?
- В какое время должны начинаться и заканчиваться отдельные работы?
- Какие работы являются критическими и должны бы ть выполнены в точно определённое графиком время, чтобы не сорвать установленные сроки выполнения проекта в целом?
- На какое время можно отложить выполнение некритических работ, чтобы они не повлияли на сроки выполнения работ?
Самый продолжительный путь сетевого графика от исходного события к завершающему называется критическим. Все события и работы критического пути называются критическими. Продолжительность критического пути и определяет срок выполнения проекта. Критических путей на сетевом графике может быть несколько. Рассмотрим основные временные параметры сетевых графиков. Обозначим $t(i,j)$ – продолжительность работы с начальным событием $i$ и конечным событием $j$. Ранний срок $t_p(j)$ свершения события $j$ – это самый ранний момент, к которому завершаются все работы, предшествующие этому событию. $t_p(j) = max ( t_p(i) + t(i,j) )$, где максимум берётся по всем событиям $i$, непосредственно предшествующим событию $j$(соединены стрелками).
Поздний срок $t_n(i)$ свершения события $i$ – это такой предельный момент, после которого остаётся ровно столько времени, сколько необходимо для выполнения всех работ, следующих за этим событием. $t_n(i) = min (t_n(j) – t(i,j))$, где минимум берётся по всем событиям $j$, непосредственно следующим за событием $i$.
Резерв $R(i)$ события $i$ показывает, на какой предельно допустимый срок может задержаться свершение события без нарушения срока наступления завершающего события: $R(i) = t_n(i) – t_p(i)$. Критические события резервов не имеют.
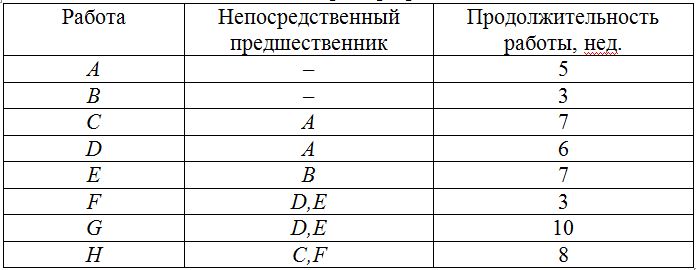
Для управления проектами с неопределённым временем выполнения работ наиболее широкое применение получил метод оценки и пересмотра проектов, рассчитанный на использование вероятностных оценок времени выполнения работ. Для каждой работы вводят три оценки:
- оптимистическое время $а$ – наименьшее возможное время выполнения работы;
- пессимистическое время $b$ – наибольшее возможное время выполнения работы;
- наиболее вероятное время $t$ – ожидаемое время выполнения работы в нормальных условиях.
Отсюда находят ожидаемое время выполнения работы:
$t=\frac {a+4m+b}{6}$ и дисперсию ожидаемой продолжительности $t$: $δ^2=(\frac {b-a}{6})^2$
После этого находят критический путь сетевого графика.
Параметры работ.
Если в сетевом графике лишь один критический путь, то его легко отыскать по критическим событиям (событиям с нулевыми резервами времени). Ситуация усложняется, если критических путей несколько. Ранний срок начала работы $(i, j)$ совпадает с ранним сроком свершения событий $i$: $t_{рн}(i, j) = t_р(i)$. Ранний срок окончания работы $(i, j)$ равен сумме $t_р(i)$ и $t(i, j)$: $t_{р0}(i, j) = t_р(i) + t(i, j)$. Поздний срок начала работы $(i, j)$ равен разности $t_n(j)$ (позднего срока свершения события $j$) и $t (i, j)$: $t_{пн}(i, j) = t_n(i) –t(i, j)$. Поздний срок окончания работы $(i, j)$ совпадает с $t_n(j): t_{n0}(i, j) = t_n(j)$. Полный резерв времени $R_n(i, j)$ работы $(i, j)$ – это максимальный запас времени, на который можно задержать начало работы или увеличить её продолжительность, при условии, что весь комплекс работ будет завершён в критический срок: $R_n(i, j) = t_n(j) – t_р(i) – t (i, j) = t_{n0}(i, j) – t_{р0}(i, j)$. Свободный резерв времени $R_с(i, j)$ работы $(i, j)$ – это максимальный запас времени, на которое можно отсрочить или (если она началась в свой ранний срок) увеличить её продолжительность при условии, что не нарушатся ранние сроки всех последующих работ: $R_с(i, j) = t_р(j) – t_р(i) – t (i, j) = t_р(j) – t_{р0}(i, j)$. Критические работы, как и критические события, резервов не имеют.
Управление запасами
верх
Рассматривается модель одиночного склада. Считается, что на складе хранится запас однотипных изделий (однономенклатурный запас). Спрос на эти изделия может быть постоянным или случайным. Склад может пополняться либо периодически (циклическая модель), либо при снижении запасов до некоторого порогового уровня (уровневая модель). Объём заказа – это количество заказываемых изделий. Уровень повторного заказа – количество изделий на складе, при котором подаётся заказ на новые изделия. Время поставки заказа может быть либо мгновенным, либо фиксированным, либо случайным. Штраф за дефицит – это убытки, связанные с отсутствием запаса. За хранение каждой единицы запаса на складе берётся определённая плата. Стоимость подачи заказа – это накладные расходы, связанные с реализацией заказа, с затратами на подготовительно-заготовочные операции, которые не зависят от объёма заказа. Для основной модели управления запасами принимается:
- Спрос равномерный и постоянный.
- Время поставки заказа постоянно.
- Отсутствие запасов на складе недопустимо
- Каждый раз заказывается постоянное количество – оптимальный размер заказа.
Решением этой оптимизационной задачи будет значение $q=\sqrt{\frac {2C_0D}{C_h}}$
- $q$ – оптимальный размер заказа;
- $С_0$ – стоимость подачи заказа;
- $D$ – годовой спрос на изделия;
- $С_h$–плата за хранение единицы запаса.
Технологический процесс может быть организован на основе производства партии продукции: чередование процессов производства и реализации произведённого. То есть надо произвести определённое количество продукции, остановить производство, реализовать произведённую продукцию и вновь запустить производство. Тогда решением задачи будет $q=\sqrt{\frac {2C_sD}{C_h}}$
- $q$ – экономический размер партии;
- $C_s$– стоимость организации производственного цикла (фиксированные издержки производства).
Очень часто, если заказываемое количество товара больше определённого числа, предоставляется скидка. В этом случае снижаются расходы на закупку, но увеличиваются затраты на хранение продукции. рассчитывать издержки с учётом скидки на продукцию. Если разрешить использование продукции по мере её производства, тогда при темпе производства продукции Ритемпа её использования D издержки будут включать в себя стоимость организации технологического процесса и хранения продукции. Решением этой задачи будет $q=\sqrt{\frac {2C_0D}{C_h}}*\sqrt{\frac {p}{P-D}}$
- $q$ – экономический размер партии.
В основной модели принимается правило: фиксированный заказ в фиксированное время. На практике спрос часто не является постоянным, поэтому основная модель должна быть изменена под определённые нужды. Самое простое, что можно сделать, – отказаться от одного из двух заявленных вначале условий.
- Случай 1. Фиксированный заказ в случайное время.
Случай 2. Случайный заказ в фиксированное время.
Как только на складе запасы понизятся до некоторого заданного заранее уровня повторного заказа, подаётся заказ на фиксированное количество единиц. Это – уровневая система Она позволяет реагировать на колебания спроса и подходит для самых разных категорий запасов, но при большом ассортименте продукции действует с перегрузкой.
Заранее определяется, в какие моменты времени будут сделаны заказы. Обычно они выбираются с определённой периодичностью. При наступлении этих моментов подаются заказы, объём которых равен разности между заранее выбранным числом и количеством единиц на складе в тот момент. Это – циклическая система повторного заказа. Она позволяет добиваться скидок за оптовые закупки, способствует ритмичной работе отдела закупок, но не способна реагировать на колебания спроса. Средний размер запаса при использовании циклической системы повторного заказа больше, чем при использовании уровневой системы повторного заказа.
Рассмотрим подробнее уровневую систему повторного заказа. Чтобы учесть непостоянство спроса, вводят резервный запас. Тогда общие издержки будут состоять из издержек на подачу заказов, хранения основного запаса, хранения резервного запаса и штрафа за дефицит. Считая вначале, что спрос постоянный, при помощи основной модели находим оптимальный размер заказа $q_0$. Именно такое количество продукции мы и будем заказывать каждый раз. Оптимальный размер заказа позволит вычислить первые две составляющие для издержек. Чтобы выбрать величину резервного запаса, следует учесть: чем больше (меньше) резервный запас, тем меньше (больше) штраф за дефицит и тем больше (меньше) стоимость хранения резервного запаса. Методом проб и ошибок мы должны подобрать резервный запас, минимизирующий две последние составляющие в выражении для общих издержек. Иногда на практике ставят целью достижение минимального уровня обслуживания. В этом случае задаётся вероятность нехватки запасов в течение цикла. Тогда минимальный уровень обслуживания находят как разницу между единицей и вероятностью нехватки запасов. По уровню обслуживания находим необходимый резервный запас. Более высокий уровень обслуживания означает более высокий резервный запас. Но издержки на поддержание большого резервного запаса могут быть очень высокими. В этом случае общие издержки исчисляются как сумма издержек на подачу заказов, хранения основного запаса и хранения резервного запаса. Целью построенной теории была минимизация издержек. Предлагаемые модели достаточно упрощенные. Если необходимо рассмотреть более сложные ситуации, то следует воспользоваться имитационным моделированием.